Fluid Physics

8.292J/12.330J

 

Problem Set 2 Solutions

 

1. A shallow layer of Euler fluid of depth  in a uniform gravitational field, given by acceleration , flows from left to right with velocity  and encounters a smooth bump of height . The bottom returns to its initial height rightward of the bump. Consider the flow to be two-dimensional (i.e. without variation in the horizontal direction normal to the flow). With one exception noted below, the flow can be considered steady.  We define a nondimensional number  (called the Froude number):

The flow can assume one of two configurations, as illustrated below:

 

                                                                 

                                                                        (a)

 

 

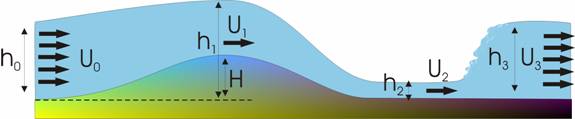
                                                                        (b)

 

In regime (b), a hydraulic jump (a stationary bore) occurs downstream of the bump; the flow near it is turbulent and dissipative.

 

 

a.)  For each of the two regimes, find expressions for  and .

 

Solution: Mass conservation demands that

 

(1)

 

while conservation of energy leads to

 

(2)

Eliminating  between the above gives

 

(3)

Clearly, one solution of the above, corresponding to regime (a), is simply

 

.

The other solution is one or the other root of what is left when  is factored out of (3):

 

.

Clearly, the negative root is unphysical, giving

 

.

(4)

Using (1) to solve for the fluid depth gives

 

.

(5)

Note that to be consistent with the way we drew regime (b),  and thus, from (5), we have . Thus we do not expect to find regime (b) for .

 

 

 

 

 

 

 

 

b.)  For regime (b), also find expressions for  and .

 

Across a hydraulic jump, mass is conserved, giving

 

,

(6)

 

but because of turbulent dissipation, energy is not conserved. On the other hand,

there is no surface drag in this region of the flow, and so vertically integrated momentum must be conserved. This means that the change in vertically integrated momentum across the hydraulic jump must equal the vertically integrated pressure difference across the jump. As demonstrated in class, this gives

 

(7)

or using (6) to eliminate ,

(8)

Ignoring the trivial solution  results in

 

(9)

The physical root of (9) is just

 

(10)

 

and using (6), the corresponding solution for  is

 

(11)

                                                                       

 

 

 

 

c.)  Find approximate expressions for  and  in the limit that  is very small.

 

Mass conservation gives

 

(12)

while conservation of energy gives

 

(13)

For convenience, nondimensionalize as follows:

 

and

Using these, and eliminating  using (12) gives

 

(14)

where  is the Froude number of the oncoming flow. In the small  limit, we look for solutions to order  of the form

 

Substituting this into (14) and collecting terms of order one and order  gives

 

and

so that, to order ,

 

(15)

 

                                                                       

Using (12), the corresponding solution for , to order , is

 

(16)

Thus, for small , the flow dips and accelerates over the hill. Note that the solution only makes sense for ; i.e., the hill is not as high as the oncoming flow.

 

d.)  Find approximate expressions for  and  in the limit that  is very large.

 

In the large  limit, we look for solutions, to order 1/ , of the form

 

Substituting into (14) an collecting like powers of 1/  gives

 

so that

 

(17)

The corresponding solution for , from (12), is

 

(18)

Thus, in the limit of large , the flow slows and rises at it approaches the hill.

 

e.)  Extra credit: For regime (b), find an expression for the net horizontal force on the bump, being sure to indicate which direction it acts.

 

The vertically integrated pressure upstream of the hill is

 

while downstream of the hill it is

 

.

 

On the other hand, the change of the vertically integrated flow momentum is

 

Comparing the momentum change to the sum of the pressure forces, it is evident that there is a missing force, given by the upstream pressure, minus the downstream pressure, minus the momentum change:

 

(19)

where we have made use of (1). Making use of (1) again as well as (2), we can write (19) as

 

(20)

This gives the net force per unit length of the hill as a function of the upstream fluid depth and the Froude number of the oncoming flow.

 

Oddly, this expression does not appear to depend on the height of the hill. This together with the apparent singularity of (15) and (16) when  suggests that there is something wrong with the way the problem has been formulated. Indeed, there is. The problem here is that is not necessarily well posed to specify both the upstream flow velocity and the depth of the upstream flow. When  is small, the "signal" of the hill can propagate indefinitely upstream, altering the upstream condition. Thus this apparently simple problem contains several interesting subtleties.

 

2a.  A barge, floating on a pond, is equipped with a pump which takes water from the pond and pumps it out through a hose fitted with a nozzle (a). The water may be idealized as an Euler fluid for this problem. The density of the water is , the cross-sectional area of the end of the nozzle is , and the velocity of the water as it exits the nozzle is . Find the force on the barge.

 

       

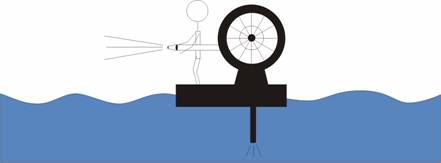
   (a)

 

 

The total change in the horizontal momentum flux is simply

 

that is the net horizontal force acting rightward on the barge.

 

2b. Consider the same problem as in 2a, but this time the pump is located on a dock (fixed to the ground; see (b)). For the purposes of this problem you may neglect gravity and assume that there are no tensile forces acting on the hose. What is the force on the barge? How might your answer change if you allow for friction of the water flowing through the hose?

 

     

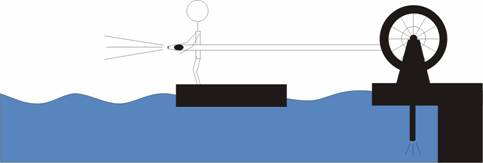
                                                        (b)

 

This is a subtle problem. The net reaction force is still that given in (a) above, but where is it actually felt?

 

One way to think about this problem more easily is to move the pump down the pipe, so the configuration looks like

 

      

 

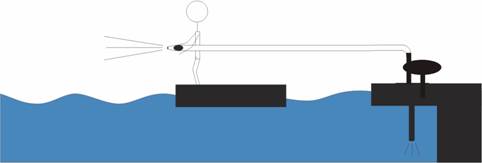
Now suppose that the cross-sectional area of the hose (before it enters the nozzle) is  and the velocity of the water in the hose is . From mass conservation, we have that . Now the change in horizontal momentum of the water going around the bend in the hose is just . This must be the rightward force acting on the dock. Since the net force acting rightward on the whole system is , the force on the barge is the difference between these two:

 

Thus if there is no nozzle on the hose (  ), there is no force on the barge.

 

If we add friction to the problem, the water flowing through the hose will exert a leftward force which must be added to the reaction force. Thus, in the case of no nozzle, there will actually be a leftward force on the barge, when friction is considered.

 

3. (Extra credit)  Consider the problem described in problem 2b, but allow for gravity, so that the hose sags. Assume that the hose has infinite tensile strength (it cannot be compressed or extended along its length) but has no resistance to bending. Neglect friction of the flowing water. What is the force on the barge?  (Note: to get a quantitative answer, you might want to consider special configurations of the hose.)

 

Suppose the hose has the shape shown below:

 

       

 

 

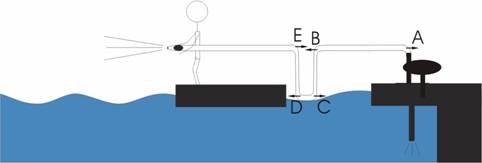
The hose is assumed to have the same diameter everywhere except in the nozzle. Note that the change in horizontal momentum at points A and B are equal and opposite, as are the changes at points C and D. Since the hose has tensile strength, these forces cancel each other. Thus the only uncompensated forces are at point E and at the nozzle. In this configuration, all the force must be taken up by the barge, and so the answer is the same as in part (a) above, namely .