Problem Set 3

1. Consider the steady hydrostatic flow of a fluid at constant velocity, , and with constant buoyancy frequency, , over two-dimensional, sinusoidal topography of amplitude and wavelength , as illustrated below:

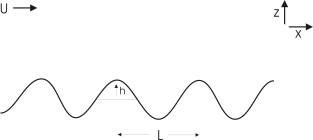
The flow extends indefinitely in the z direction, and the mean density of the fluid is .

a.) Making the small amplitude approximation, solve for the flow components u and w as functions of x and z.

b.) By considering the rate at which horizontal momentum is transported downward through the fluid, derive an expression for the drag on the surface, per unit wavelength .

c.) (Extra Credit) Solve the same problem but for an isolated ridge whose height is given by

where is the amplitude and is a width scale. This time, calculate the total drag on the mountain. Hint: The Fourier transform of is

2. Tornadoes are intense atmospheric vortices, often made visible by very small water droplets that condense as air swirls into the vortex. The object of this exercise is to make certain deductions about the distribution and speed of tornadic winds from observations of the geometry of the condensation funnel. A key feature of the atmosphere in the region between the ground and the base of the cloud from which the tornado issues is that it has an adiabatic temperature profile, which means that 1.) All air at the same pressure has the same temperature, and 2.) All air at any pressure, when moved adiabatically to a fixed reference pressure, has the same temperature. Another feature of this part of the atmosphere is that the mass fraction of water vapor (known as the specific humidity, q ) is nearly constant.

a.) The saturation specific humidity, q* is a function of temperature and pressure only. When its value becomes as small as q, water vapor condenses. The quantity q is nearly constant following samples of air as they move along. Show that under these circumstances, the outer boundary of the condensation funnel is a surface of constant pressure.

b.) Consider a point at the surface of the earth some distance from the tornado, in a reference frame moving with the vortex. In this reference frame the tornado may be approximated as a steady, adiabatic system. Assume that the wind speed is very small at this point and that the atmosphere is hydrostatic between this point and the base of the thunderstorm cloud. Also assume that air at this point swirls into the vortex along the ground which, being Kansas, can be considered a level surface which exerts no frictional drag on the flow. This flow of air is adiabatic as well. Find an expression for the magnitude of the air velocity at the point that the outer boundary of the condensation funnel contacts the ground, as a function of the altitude of the cloud base above the ground far from the tornado. The acceleration of gravity may be assumed constant.

c.) To a very good approximation, the component, V, of air flow that travels around the vortex center is in a state of centripetal balance with the radial pressure gradient:

Assume that V varies inversely with radius outside the condensation funnel and does not vary with altitude, and that the flow near the tornado is hydrostatic. Derive an expression for the shape of the outer edge of the condensation funnel.