Fluid Physics
8.292J/12.330J
Problem Set 5
Solutions
1. Consider the flow of an Euler fluid in the x direction given by
for
for
for
This flow does not vary in x or in z. Determine the propagation and/or growth/decay of small perturbations to this flow that are sinusoidal in the x direction and which do not vary in the z direction.
Solution:
We
begin with the general equation for the structure in of two-dimensional disturbances:
|
|
Note that, as in the classical Rayleigh problem, the second term in brackets vanishes within each of the three regions of the flow. As in that problem, we find solutions to (1) within each region and match across the two boundaries separating the regions.
The
solution to (1) in each region, which satisfy
the boundary conditions at have the form
|
|
The
first matching condition is to match the displacement in ,
which in this problem is equivalent to matching
itself. The second condition is to match the
fluid pressure, which can be found from the original linearized equations or
from integrating (1) in
to get continuity of
|
|
|
Applying
these two matching conditions at and
to (2) yields the dispersion relation
|
|
There
is a range of in which the argument of the square root in (3) is negative; in this range,
had an imaginary part and the solutions are
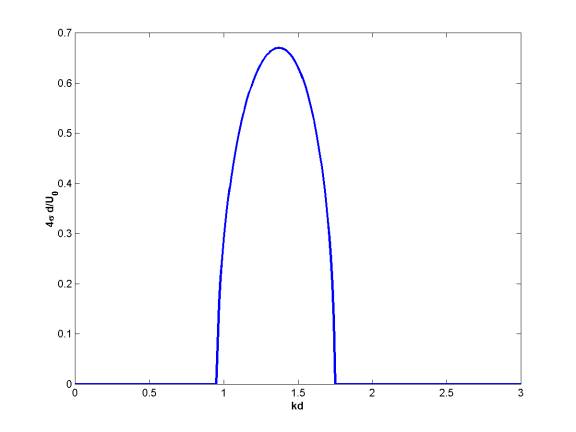
exponentially growing or decaying. The figure below shows the positive root of
the nondimensional growth rate,
:
The
upper root of the solution for the nondimensional phase speed over a larger
range of is shown below:
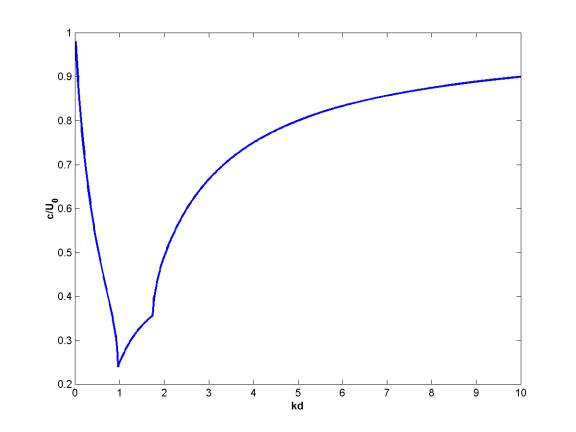
Note that the phase speeds are always smaller than the peak velocity of the mean flow.
Like the classical Rayleigh problem, the two transition regions of the mean flow support Rossby waves which, in a narrow regime of wavelengths, may interact unstably to produce exponentially amplifying disturbances.
2. Consider a
cylindrical tank of radius of an incompressible fluid, rotating at
angular velocity
and subject to a uniform gravitational
acceleration,
,
downward along the rotation axis, as pictured below:
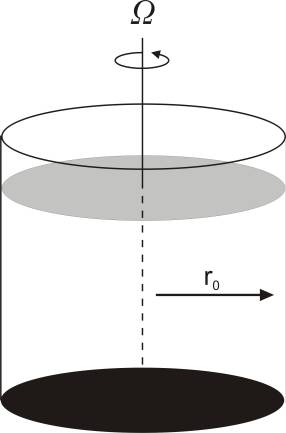
a.) Derive an expression for the shape of the free surface.
Solution: In equilibrium, the radial pressure gradient acceleration balances the outward centrifugal acceleration:
|
|
|
which, when integrated, yields
|
|
|
where
is the height of the surface at the center.
Thus the surface is parabolic.
b.) Suppose that the bottom of the cylinder is
stationary, so that the fluid is moving with respect to it. This relative
motion exerts a torque on the fluid, but we can consider that this torque is
confined to a thin layer adjacent to the bottom of the tank. We further assume
that the flow remains circularly symmetric. Taking to be the angular momentum of the fluid per
unit mass,
where
is the tangential component of velocity. An
equation for the conservation of angular momentum in the thin boundary layer is
|
|
|
where
is called the "frictional stress".
We assume that this stress vanishes at the top of the boundary layer (in fact,
that is the definition of the top of the boundary layer), and that the stress
at the surface is given by
|
|
|
It can be shown that if the boundary layer is sufficiently thin, the right side of (4) will be large compared to the first term on the left, and so, to a good approximation,
|
|
|
We
can further assume that does not vary with altitude within the thin
boundary layer.
The incompressible mass continuity equation in cylindrical coordinates is
|
|
|
Taking
to vanish at the bottom of the tank, use (5) - (7) to find an
expression for
at the top of the boundary layer, in terms of
the radial distribution of
(or
). Evaluate this expression for the case that
.
Solution: If we integrate (6) through the depth of the boundary layer and apply (5), we get
|
|
where h is the boundary layer depth. Now integrating (7) over the depth of the boundary layer gives
|
|
where is the vertical velocity at the top of the
boundary layer. Combining (8) and (9)
gives
|
|
In the case that ,
this gives
|
|
Here it is seen that the vertical velocity is, in this case, proportional by a constant to the swirling velocity component.
c.) One
problem with this solution is that it requires radial flow through the outer
wall of the tank. Consider instead and unbounded tank (let ), but use the following velocity
distribution:
|
|
|
where
is a number between zero and one. Find the
depth-averaged radial velocity in the boundary layer and the vertical velocity
at the top of the boundary layer.
Solution: For the interior part of this flow, the solution is, of course, given by (8) and (11). Substituting the second part of (12) into (8) and (10) gives
|
|
and
|
|
(14) |
d.)
Extra credit: Considering the depth of
the tank to be ,
which may be taken to be large compared to the thickness of the boundary layer,
find an expression for the instantaneous rate of decrease (with time) of
angular momentum of the fluid above the boundary layer. What value of
makes this rate of decrease independent of
radius?
Solution: According to the Taylor-Proudman Theorem, in a
slowly changing, rotating, incompressible and inviscid fluid, the velocity
should not vary along the direction of the rotation vector. Accordingly, above
the boundary layer in the present flow, the radial and swirling velocity
components should not vary with height. If we use to denote the radial velocity above the
boundary layer, mass conservation tells us that there can be no net mass flow
across any cylindrical surface, so that
|
|
(15) |
where
is the fluid depth (technically, minus the
boundary layer depth, h). Applying this to the outer solution, (13), gives
|
|
Now angular momentum is conserved in the inviscid flow above the boundary layer, so the time rate of change of angular momentum is given by
|
|
Substituting
(16) for and using (12) to calculate
in (17) gives
|
|
(18) |
Clearly,
when ,
this spin down rate is independent of radius.