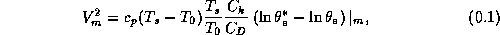
Maximum Intensity Estimation
Kerry A. Emanuel
Massachusetts Institute of Technology
The upper bound on tropical cyclone intensity is calculated using sea surface temperature and atmospheric thermodynamic profiles from the latest output of the Medium Range Forecasting (MRF) model from the National Centers for Environmental Prediction. The technique represents a generalization of that presented in Emanuel (1995; hereafter, E95) to the case of an open-cycle heat engine. The description presented by Emanuel (1995) has been further modified to account for dissipative heating, which had been neglected in earlier treatments. These modifications are described in Bister and Emanuel (1998). The input to the scheme at each grid point is the sea surface temperature and vertical profiles of pressure, temperature, and mixing ratio. (The FORTRAN subroutine is available from the author.)
For the purposes of this calculation, the work done against friction in the hurricane outflow is ignored. If the size of the storm is known, this work can be estimated, but it is usually very small unless the storm has an exceptionally large diameter (Emanuel, 1986). We also assume that at maximum intensity, the anticyclone at the storm top is fully developed (zero absolute vorticity) and that the gradient wind may be approximated by the cyclostrophic wind at the radius of maximum winds. When these conditions are satisfied, the thermal wind equation can be combined with an equation governing entropy in the boundary layer in regions near the eyewall where little entrainment of dry air through the top of the boundary layer occurs, resulting in:
where 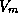 is the maximum gradient wind speed,
is the maximum gradient wind speed,
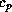 is the heat capacity at constant pressure,
is the heat capacity at constant pressure, 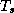 is the
ocean temperature,
is the
ocean temperature, 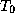 the mean outflow temperature,
the mean outflow temperature, 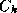 the
exchange coefficient for enthalpy,
the
exchange coefficient for enthalpy, 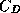 the drag coefficient,
the drag coefficient,
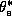 the saturation equivalent potential temperature at the
ocean surface, and
the saturation equivalent potential temperature at the
ocean surface, and 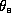 the boundary layer equivalent potential
temperature. The last factor in (1) is evaluated at the radius of
maximum winds. This expression is the dimensional equivalent of Eq.
(13) of E95, and can also be written
the boundary layer equivalent potential
temperature. The last factor in (1) is evaluated at the radius of
maximum winds. This expression is the dimensional equivalent of Eq.
(13) of E95, and can also be written
where  is the entropy (
is the entropy (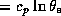 ) and the closed cycle is
for a parcel beginning at the ambient boundary layer value of
) and the closed cycle is
for a parcel beginning at the ambient boundary layer value of
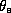 and winding up at saturation. Entropy is acquired at
temperature
and winding up at saturation. Entropy is acquired at
temperature 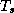 and exported at temperature
and exported at temperature 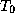 . It is
important to note that (2) does
not imply that air parcels actually become saturated at sea
level under the eyewall.
. It is
important to note that (2) does
not imply that air parcels actually become saturated at sea
level under the eyewall.
The integral in (2) is also equal to the convective available potential energy (see Emanuel, 1994, Eq. 6.4.2). Thus (1) can be written
where 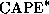 is the convective available potential energy of
air lifted from saturation at sea level in reference to the
environmental sounding, and
is the convective available potential energy of
air lifted from saturation at sea level in reference to the
environmental sounding, and 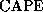 is that of boundary layer
air. Both quantities are evaluated near the radius of maximum wind.
is that of boundary layer
air. Both quantities are evaluated near the radius of maximum wind.
To evaluate (3) it is first necessary to determine the surface
pressure at the radius of maximum winds, needed to calculate the
saturation mixing ratio necessary for 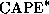 . To do so, we
use a combination of gradient wind balance and thermal wind balance
in the outer region of the hurricane. This is equation (6) of E95,
whose dimensional equivalent (assuming cyclostrophic balance at the
radius of maximum winds) is
. To do so, we
use a combination of gradient wind balance and thermal wind balance
in the outer region of the hurricane. This is equation (6) of E95,
whose dimensional equivalent (assuming cyclostrophic balance at the
radius of maximum winds) is
where 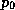 is the ambient surface pressure and
is the ambient surface pressure and 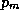 is the surface
pressure at the radius of maximum winds.
is the surface
pressure at the radius of maximum winds.
To calculate  , the mixing ratio and temperature of the
boundary layer under the eyewall is needed. Following E95, we assume
that the surface temperature is
, the mixing ratio and temperature of the
boundary layer under the eyewall is needed. Following E95, we assume
that the surface temperature is 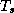 and that the relative humidity
is constant from the outer region to the outer edge of the eyewall.
Since the pressure under the eyewall is lower than ambient, this
entails a small inward increase in mixing ratio. (Experiments
assuming constant mixing ratio rather than constant relative humidity
yield only slightly different results.) For this reason,
and that the relative humidity
is constant from the outer region to the outer edge of the eyewall.
Since the pressure under the eyewall is lower than ambient, this
entails a small inward increase in mixing ratio. (Experiments
assuming constant mixing ratio rather than constant relative humidity
yield only slightly different results.) For this reason,
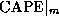 is a little larger than the
is a little larger than the 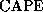 of ambient
boundary layer air. The assumption of constant relative humidity in
the outer region boundary layer is well supported by numerical
simulations.
of ambient
boundary layer air. The assumption of constant relative humidity in
the outer region boundary layer is well supported by numerical
simulations.
Given a value of 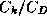 , the sea surface temperature, and an
ambient profile of virtual temperature, (3) and (4) constitute closed
relations for
, the sea surface temperature, and an
ambient profile of virtual temperature, (3) and (4) constitute closed
relations for 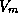 and
and 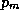 .
. 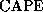 is calculated by a
reversible adiabatic parcel lifting algorithm. Owing to the pressure
dependence of
is calculated by a
reversible adiabatic parcel lifting algorithm. Owing to the pressure
dependence of 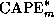 and
and  , (3) and (4) must
be solved iteratively. This always converges unless one is in the
``hypercane'' regime.
, (3) and (4) must
be solved iteratively. This always converges unless one is in the
``hypercane'' regime.
Lastly, we estimate the central pressure as in E95 by assuming that the flow inside the radius of maximum winds is in solid body rotation and cyclostrophic balance. This yields the relation
where 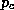 is the central surface pressure.
is the central surface pressure.
In the output of the subroutine used to calculate 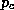 and
and 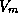 ,
the latter has been reduced by 20% to reflect the typical
relationship between gradient winds and actual surface winds.
,
the latter has been reduced by 20% to reflect the typical
relationship between gradient winds and actual surface winds.
References
Emanuel, K. A., 1986: An air-sea interaction theory for tropical cyclones. Part I. J. Atmos. Sci., 42, 586-604.