In the previous section, we noted that the radiative equilibrium distribution in a simple model gives thermal disequilibrium between the surface and the immediate overlying atmosphere, implying that some convective heat transport will occur. In fact, the entire atmosphere shown in Figure 2.3 must convect, because it's vertical temperature distribution is unstable. Convective instability is easy to understand. Suppose we take a test sample from the lower layer in Figure 2.3 and lift it by a reversible adiabatic process up to the middle of the upper layer. If the density of the lifted sample is less than that of the surrounding air, then buoyancy will accelerate it upward, in the same direction as the original displacement. If an adiabatic displacement in an equilibrium system results in a force in the same direction as the displacement, we say that that displacement is unstable. Let's calculate the specific volume (or inverse density) of the adiabatically displaced test sample and compare it to the specific volume of the upper layer. If the sample has a greater specific volume, its density will be less and the displacement will thus be unstable.
The specific volume of the sample may be expressed as a function of any two
other state variables. Since entropy is conserved in a reversible adiabatic
displacement, it makes a convenient variable to work with. Thus we express the
specific volume, 
, as
where 
is the specific entropy and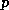 
is the pressure. Now we are comparing
the specific volume of the displaced sample with that of its surroundings at the same pressure. So we can write the difference, if it is small, as
The partial derivative in (18) is taken at constant pressure. We can now use one of Maxwell's relations, which can be derived from the First Law of Thermodynamics:
Since the adiabatic lapse rate,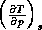 
, is always positive, (20) shows that the atmosphere will
be unstable if its entropy decreases upward, so that the sample displaced from
the lower to the upper layer will have an entropy that is greater than that of
the upper layer. The condition for convective instability is simply that
the entropy of the gas decreases upward along the gravitational vector.
As it turns out, the radiative equilibrium entropy distribution is unstable in the earth's troposphere. For this reason, much of the troposphere is convecting; in fact, this is part of the reason why ``weather" happens in the troposphere. But convection is a relatively fast process in the atmosphere, with characteristic time scales of a few hours. On the other hand, perturbations away from radiative equilibrium decay back to equilibrium on time scales closer to 50 days. Therefore, in a competition between the two processes, convection must ``win" in the sense that the observed temperature distribution will be much closer to convective than to radiative equilibrium.
Atmospheres in which the heat transport by radiation and convection are in
balance are said to be in radiative-convective equilibrium. As a first
cut at calculating a radiative-convective equilibrium state, we can suppose that
the temperature difference between the upper and lower layers of our simple
model is fixed, by convection, at a value of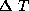 
. Figure 3.1 shows our
simple radiative-convective equilibrium model. We suppose that, in addition to
the radiative fluxes, a convective heat flux, 
, carries heat from the lower
to the upper layer, and a turbulent heat flux,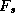 
, also carries heat from the
surface into the lower layer. The energy balances are
Surface:
Lower layer:
Upper layer:
We next impose a condition for convective neutrality:
and
Solving (21) - (25) for the various quantities gives the following solution:
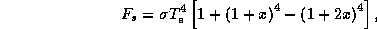
and
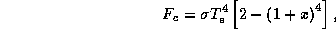
where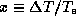 
. The condition for the viability of this
solution is that 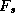and are positive. Given that 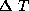is
positive, both of the convective fluxes will be positive if and only if
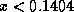. Also, we can see that the smaller the adiabatic lapse rate, to
which 
is proportional, the greater the convective heat fluxes must be.
In the earth's atmosphere, the actual radiative-convective equilibrium state is far more complex than is captured by these simple models. For one thing, the emissivity of each infinitesimal layer is a strong function of the concentration of absorbing gases and clouds, and the principal absorbers, water vapor and clouds, are strong functions of the convection, which is part of the response of the system. Secondly, the convection that actually occurs is moist convection, in the form of cumulus and cumulonimbus clouds, so we have to redefine the entropy to take into account the presence of water substance. Fortunately, we can safely assume that, in clouds, the liquid and vapor phases of water are in thermodynamic equilibrium, and that, to a good approximation, the condition for convective neutrality is that the saturation entropy is constant with height. The saturation entropy is given by (9) but with the vapor pressure and specific humidity replaced by the values they would have were the sample saturated with water at the same temperature and pressure:
Since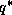 
is just a function of 
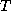and 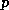, the constancy of 
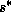is
(26) just gives a relationship between 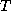and 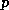which is called the
moist adiabatic lapse rate.
In the tropics, actual temperature lapse rates are usually very close to their adiabatic values. Figure 3.2 shows a comparison between an average temperature sounding from the tropical western South Pacific and an adiabatic temperature profile.
In the real world, large-scale atmospheric and oceanic circulations transport heat laterally between high and low latitudes. This reduces the temperature of the Tropics to values less than they would be in strict radiative-convective equilibrium, but the latter state remains a good first approximation to the physical state of the tropical atmosphere-ocean system.
Figure 3.3 summarizes the energy balance of the global atmosphere. Of 100 units of incoming solar radiation, about 30% is reflected back to space by the surface, by clouds, and by the atmosphere itself. A small amount of solar radiation is directly absorbed in the atmosphere, mostly by water vapor and by clouds. The back radiation of the atmosphere to the earth is so large - larger than the incoming solar radiation reaching the surface - that there must be large convective heat transport away from the surface. It is conventional to divide this turbulent heat transport into two parts: sensible and latent flux. The latter is proportional to rate of evaporation of water from the surface into the overlying air. Note that most of the flux is in the form of latent heat flux. In fact, in the Tropics, the latent heat flux is very much larger than either the sensible flux or the net longwave radiative flux from the surface. So, to a good approximation, absorption of solar radiation by the tropical oceans is balanced by cooling by evaporation.
To maintain the large evaporation rates, the tropical atmosphere and ocean must
exist in a state of considerable thermodynamic disequilibrium. To see this, it
is helpful to examine a conventional formula for estimating the rate of
evaporation,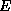 
, from the ocean to the atmosphere:
where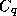 
is a dimensionless exchange coefficient, 
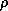is the air
density,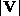 
is the magnitude of the wind speed, 
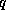is the specific
humidity of the air, and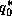 
is the saturation specific humidity of air at
sea surface temperature and pressure. It is conventional to evaluate all the
quantities in (27), except for 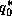, at an altitude of 10 meters
above the surface. (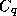 is calibrated to this altitude.)
One can see from (27) that to maintain large evaporation rates, one
must have a large degree of thermodynamic disequilibrium, as given by the term
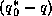, and this degree of disequilibrium is inversely proportional to the
average wind speed, for a given evaporation rate. Tropical cyclones use this
disequilibrium to fuel their enormous power consumption, as we illustrate in the
next lecture.
