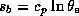 ) in the subcloud layer:
) in the subcloud layer:
Most convection in the tropics originates from the comparatively thin subcloud layer, for it is this layer that receives direct heat input from the underlying surface. At the same time, the thermodynamic disequilibrium between the subcloud-layer air and the underlying ocean is large enough that, were they unopposed, surface fluxes would bring the subcloud entropy into equilibrium with the surface in about 12 hours. In nature, however, the surface enthalpy fluxes are very nearly balanced by the entrainment of low-entropy air through the top of the layer. In undisturbed conditions, this entrainment is accomplished by small-scale turbulence acting on a pronounced negative jump of entropy across the top of the layer, while in regimes experiencing deep convection, convective downdrafts are the principal agents for importing low-entropy air.
The near balance of the subcloud-layer entropy budget was used by
Emanuel (1993) to determine the convective updraft mass flux out of
the boundary layer, in a simple model of intraseasonal oscillations
in convecting atmospheres. Recently, Raymond (1995) has more
thoroughly discussed the physical basis for such a representation of
convection. The basic idea can be illustrated using the vertically averaged
budget of entropy (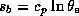 ) in the subcloud layer:
) in the subcloud layer:
where  is the depth of the subcloud layer,
is the depth of the subcloud layer,
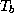 and
and 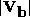 are the near-surface air temperature and wind
speed,
are the near-surface air temperature and wind
speed, 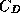 is an exchange coefficient,
is an exchange coefficient, 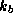 is the enthalpy of air
near the sea surface (
is the enthalpy of air
near the sea surface (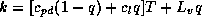 , where
, where 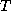 and
and 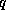 are the
temperature and specific humidity,
are the
temperature and specific humidity, 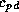 and
and  are the heat capacity at
constant pressure of dry air and the heat capacity of liquid water,
respectively, and
are the heat capacity at
constant pressure of dry air and the heat capacity of liquid water,
respectively, and 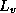 is the latent heat of vaporization),
is the latent heat of vaporization),
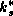 is the saturation enthalpy at sea surface temperature,
is the saturation enthalpy at sea surface temperature, 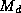 is the convective downdraft volume flux at cloud base,
is the convective downdraft volume flux at cloud base, 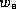 is the
vertical velocity outside of the clouds at the top of the subcloud
layer (assumed negative here),
is the
vertical velocity outside of the clouds at the top of the subcloud
layer (assumed negative here), 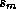 is the entropy of air above the
subcloud layer, and
is the entropy of air above the
subcloud layer, and 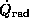 is the radiative cooling in
the subcloud layer. It has been assumed that dry
turbulence at the top of the subcloud layer and convective downdrafts
both import the same value of entropy,
is the radiative cooling in
the subcloud layer. It has been assumed that dry
turbulence at the top of the subcloud layer and convective downdrafts
both import the same value of entropy, 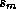 , into the subcloud
layer; this has been done for simplicity but is not necessary for the
following development.
, into the subcloud
layer; this has been done for simplicity but is not necessary for the
following development.
The quasi-equilibrium assumption for the subcloud layer entropy neglects the time tendency of entropy and the radiative cooling terms in comparison to the surface and downdraft fluxes, which are thus assumed to be in equilibrium, yielding
At the same time, mass continuity at the top of the subcloud layer demands that
where 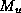 is the net convective updraft mass flux at cloud base,
and
is the net convective updraft mass flux at cloud base,
and 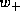 is the total (large-scale) vertical velocity at cloud base.
Combining (3) and (2) gives
is the total (large-scale) vertical velocity at cloud base.
Combining (3) and (2) gives
subject to 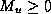 . (This is nearly identical to Eq. (11) of
Emanuel, 1993.) Thus the convective updraft mass flux is related to
the mean ascent at the top of the subcloud layer and the surface
enthalpy flux. In most tropical circulations, the contribution to
. (This is nearly identical to Eq. (11) of
Emanuel, 1993.) Thus the convective updraft mass flux is related to
the mean ascent at the top of the subcloud layer and the surface
enthalpy flux. In most tropical circulations, the contribution to
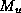 from
from 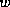 is somewhat larger than that from variable surface
fluxes, but in waves such as the Madden-Julian oscillation (MJO), the
phase of the surface flux term contributes to wave growth, while
that from
is somewhat larger than that from variable surface
fluxes, but in waves such as the Madden-Julian oscillation (MJO), the
phase of the surface flux term contributes to wave growth, while
that from 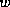 alters the phase speed of the disturbances, but does
not amplify them.
alters the phase speed of the disturbances, but does
not amplify them.
Although (4) provides a diagnostic expression for the convective updraft mass
flux at the top of the subcloud layer, the net convective mass
flux, 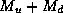 , is needed to predict temperature changes in the free
atmosphere, for it is this sum that forces compensating subsidence.
We begin by writing the equation for potential temperature just above the
top of the subcloud layer,
, is needed to predict temperature changes in the free
atmosphere, for it is this sum that forces compensating subsidence.
We begin by writing the equation for potential temperature just above the
top of the subcloud layer, 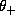 :
:
where
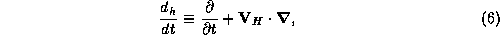
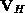 is the horizontal velocity vector, and
is the horizontal velocity vector, and 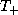 is the temperature
just above the subcloud layer.
is the temperature
just above the subcloud layer.
It is clear from (5) that a relationship between the convective
updraft and downdraft mass fluxes is needed. This must be provided,
in general, by a cloud model. For the purposes of constructing a
maximally simple model of the MJO, Yano and Emanuel (1991) and
Emanuel (1993) related 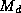 to
to 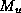 just above cloud base by
just above cloud base by
where 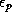 is a bulk precipitation efficiency, which is in general
a function of cloud water distributions and environmental temperature and
humidity. If all the
rain evaporates,
is a bulk precipitation efficiency, which is in general
a function of cloud water distributions and environmental temperature and
humidity. If all the
rain evaporates, 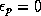 and
and 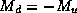 , consistent with the
fact that there is then no net latent heat release. If, on the other
hand,
, consistent with the
fact that there is then no net latent heat release. If, on the other
hand, 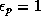 ,
, 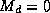 : there is no evaporation to drive a
downdraft.
: there is no evaporation to drive a
downdraft.![]() In this model,
In this model, 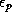 will be specified as a
function of environmental relative humidity only.
will be specified as a
function of environmental relative humidity only.
We now substitute (4) and (7) into (5) to obtain
This shows that actual temperature changes just above the top of the
subcloud layer are driven by surface enthalpy fluxes, radiative
cooling and adiabatic cooling related to large-scale ascent. Note
that the effective stratification is proportional to 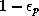 ;
Yano and Emanuel (1991) and Emanuel (1993) argue that this accounts
for the small phase speed of the MJO, consistent with observations
and with models using linearizations of the Betts-Miller cumulus
parameterization (Neelin and Yu, 1994; Emanuel et al., 1994).
;
Yano and Emanuel (1991) and Emanuel (1993) argue that this accounts
for the small phase speed of the MJO, consistent with observations
and with models using linearizations of the Betts-Miller cumulus
parameterization (Neelin and Yu, 1994; Emanuel et al., 1994).
Before proceeding, we express (8) in a slightly different form by
using the saturation entropy, 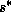 , in place of
, in place of 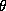 . (The
saturation entropy is the entropy the air would have were it
saturated at the same pressure and temperature; it is a state
variable and may also be expressed as
. (The
saturation entropy is the entropy the air would have were it
saturated at the same pressure and temperature; it is a state
variable and may also be expressed as 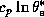 , where
, where
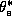 is the saturation equivalent potential temperature.) The
relationship between fluctuations at constant pressure of
is the saturation equivalent potential temperature.) The
relationship between fluctuations at constant pressure of 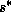 and
and
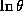 is (e.g., see Emanuel, 1994a)
is (e.g., see Emanuel, 1994a)
where 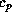 is a heat capacity at constant pressure, and
is a heat capacity at constant pressure, and 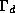 and
and
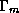 are the dry and moist adiabatic lapse rates, respectively.
Using (9), (8) may be written
are the dry and moist adiabatic lapse rates, respectively.
Using (9), (8) may be written
where 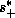 is the saturation entropy just above the subcloud layer.
is the saturation entropy just above the subcloud layer.
We now argue that to a first approximation, 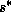 is constant through the
depth of the convecting layer. To begin with, several arguments have been
advanced (e.g. Bretherton and Smolarkiewicz, 1989) that entrainment, and
therefore mass flux,
is related to the variation of cloud buoyancy with height. This supports
the device, used in many convective schemes (e.g. Manabe et al. (1965),
Betts (1986)) of driving actual lapse rates towards moist adiabatic lapse
rates. We shall assume here that the lapse rate in the convecting layer is
maintained by convection at its moist adiabatic value. Neglecting the
direct effect of water substance on density, this is equivalent to
assuming that
is constant through the
depth of the convecting layer. To begin with, several arguments have been
advanced (e.g. Bretherton and Smolarkiewicz, 1989) that entrainment, and
therefore mass flux,
is related to the variation of cloud buoyancy with height. This supports
the device, used in many convective schemes (e.g. Manabe et al. (1965),
Betts (1986)) of driving actual lapse rates towards moist adiabatic lapse
rates. We shall assume here that the lapse rate in the convecting layer is
maintained by convection at its moist adiabatic value. Neglecting the
direct effect of water substance on density, this is equivalent to
assuming that 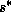 is constant with height and equal to its value,
is constant with height and equal to its value,
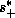 , just above the top of the subcloud layer. This assumption was
also made by Emanuel (1993). Thus (10) may be regarded as a prediction
equation for temperature throughout the depth of the convecting layer. In
general, this depth must also be predicted or diagnosed; here we take it to
have a fixed value for simplicity.
, just above the top of the subcloud layer. This assumption was
also made by Emanuel (1993). Thus (10) may be regarded as a prediction
equation for temperature throughout the depth of the convecting layer. In
general, this depth must also be predicted or diagnosed; here we take it to
have a fixed value for simplicity.
Up until now we have assumed that convection responds instantly to changes
in the large-scale forcing. But even though it is small, the time scale of
convection has been shown to have important effects in global models (Betts
and Miller, 1986) and in idealized models of intraseasonal oscillations in
the tropics (Emanuel, 1993; Neelin and Yu, 1994). We account for this time
scale here using the same approach as Emanuel (1993). We regard (4) as an
expression for the equilibrium updraft mass flux, 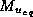 :
:
and relax the actual updraft mass flux to this value using
with 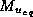 given by (11), and
given by (11), and 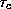 taken to
be on the order of a few hours. The saturation entropy through the depth of
the convecting layer (which is assumed equal to
taken to
be on the order of a few hours. The saturation entropy through the depth of
the convecting layer (which is assumed equal to 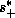 ) is then predicted
using (5), (7) and (9):
) is then predicted
using (5), (7) and (9):
It should be understood that all the quantities on the right side of (13) are to be evaluated just above the top of the subcloud layer.
Finally, it is necessary to predict the distributions of
subcloud-layer entropy, 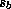 , and the entropy at the source level for
downdrafts,
, and the entropy at the source level for
downdrafts, 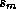 , used in (11). (In the linearized version of (11)
used by Yano and Emanuel, 1991, and Emanuel, 1993, fluctuations of
, used in (11). (In the linearized version of (11)
used by Yano and Emanuel, 1991, and Emanuel, 1993, fluctuations of
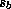 and
and 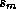 in (11) were ignored and so this was not necessary.) In
regions where it exists, convection can be assumed to tie the
subcloud-layer entropy to the value of
in (11) were ignored and so this was not necessary.) In
regions where it exists, convection can be assumed to tie the
subcloud-layer entropy to the value of 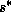 at the subcloud-layer
top, so that the subcloud-layer air is approximately neutral to small
upward displacements. In regions of strong large-scale descent,
however, deep convection may cease and in that case it is necessary
to solve the subcloud-layer entropy equation (1). In general, the
subcloud-layer entropy may always be determined by (1) subject to the
constraint
at the subcloud-layer
top, so that the subcloud-layer air is approximately neutral to small
upward displacements. In regions of strong large-scale descent,
however, deep convection may cease and in that case it is necessary
to solve the subcloud-layer entropy equation (1). In general, the
subcloud-layer entropy may always be determined by (1) subject to the
constraint
where 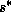 is the saturation entropy above the subcloud layer.
is the saturation entropy above the subcloud layer.
We summarize this approach to representing deep convection as follows:
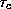 , using (12).
, using (12).
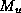 and
and 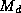 . The simplest
approach relates the two linearly; this results in Eq. (13) for the
saturation entropy,
. The simplest
approach relates the two linearly; this results in Eq. (13) for the
saturation entropy, 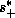 , just above the subcloud layer.
, just above the subcloud layer.
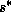 ) through
the rest of the convecting layer, it is assumed that the
layer temperature relaxes toward a moist adiabat (
) through
the rest of the convecting layer, it is assumed that the
layer temperature relaxes toward a moist adiabat (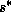 constant with
height) at some rate. Assumptions about the magnitude of this rate
vary greatly. We follow Emanuel (1993) and assume that
constant with
height) at some rate. Assumptions about the magnitude of this rate
vary greatly. We follow Emanuel (1993) and assume that 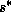 is constant with
height at all times, but relax the strict equilibrium of the
boundary layer by introducing Eq. (12).
is constant with
height at all times, but relax the strict equilibrium of the
boundary layer by introducing Eq. (12).
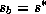 , except where large-scale
conditions prohibit deep convection, in which case the subcloud-layer
entropy budget must be explicitly calculated using (1). Both cases
may be satisfied simply by solving (1) subject to the constraint
(14).
, except where large-scale
conditions prohibit deep convection, in which case the subcloud-layer
entropy budget must be explicitly calculated using (1). Both cases
may be satisfied simply by solving (1) subject to the constraint
(14).
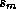 , at the
source level for convective downdrafts must be solved.
, at the
source level for convective downdrafts must be solved.
Note that point 1 is a quasi-equilibrium assumption on boundary layer entropy, which does vary slowly and is predicted according to point 6. Other aspects of this way of representing moist convection are discussed in some detail in Raymond (1995).
When a version of this simple way of representing convection is used in a model of the equatorial beta plane, linearized about mean easterly flow, unstable modes representing slow, eastward-propagating planetary Kelvin waves and westward-propagating synoptic-scale waves with structures similar to mixed Rossby-gravity modes emerge. Emanuel (1993) also showed that in order to model these properly, the small time lags over which convection relaxes the tropospheric temperature to a moist adiabat are crucial; strict quasi-equilibrium of the Arakawa-Schubert (1974) kind results in spurious high-frequency modes.
The purpose of this paper is to show that the simple way of representing convection reviewed above also performs very well in a simple hurricane model.