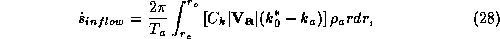
In many ways, it is easier to begin with a discussion of the energy cycle of a mature tropical cyclone. The genesis of tropical cyclones is in many ways a separate, and more difficult subject, and we shall address this in Lecture 6.
tropical cyclones can exist in a nearly steady state for many days at a time, though it is relatively unusual for them to do so. In numerical models, they can become very nearly steady. It is therefore useful to start with an idealization of the storm as an axisymmetric, steady system. This eliminates two degrees of freedom from the governing equations.
The energy cycle of a mature tropical cyclone is illustrated in Figure 4.1. Air spirals in toward the center in a turbulent boundary layer that ranges in depth from about 1 km in the outer regions to perhaps 100 m under the eyewall. During this inward trek, the air experiences little net change of its specific entropy, owing to the competing effects of enthalpy flux from the ocean, which is acting to increase the boundary layer entropy, and downdrafts associated with spiral band convection as well as turbulent entrainment at the top of the boundary layer, both of which serve to import air of lower entropy from higher up in the troposphere. But then, as air approaches the eyewall convection, the import of low entropy air from above the boundary layer diminishes, and the surface fluxes, which are very strong in the region of high winds, cause the entropy to rise quite sharply. Also, the turbulent dissipation of wind energy, which can be shown to rise as the cube of the mean wind speed, becomes very large and contributes appreciably to an increase in the entropy of boundary layer air. The essential energy input to a tropical cyclone is from large surface heat fluxes in and near the eyewall. Note that the surface enthalpy flux is the only energy source in the tropical cyclone; dissipation of kinetic energy increases the entropy of the inflowing air but does not change its total energy content.
The air then turns upward in the eyewall and flows out to large radii. Referring to the control volume illustrated in Figure 4.1, the input of energy from the sea surface is balanced by export through the outer wall of the control volume.
In essence, the mature tropical cyclone is a fine example of a Carnot heat engine, except that the engine does no work on its environment; instead, the available work is locally dissipated and a fraction of the dissipated energy is recycled into the engine.
Now consider the entropy budget for the control volume. There are two main, distinct entropy sources: those associated with the import and export of heat through the walls of the control volume, and dissipative heating in the boundary layer. (There are also a myriad of secondary irreversible entropy sources having to do with the fall and evaporation of precipitation, turbulent mixing of air with disparate thermodynamic properties, production of sea spray, etc., but we will ignore these here.) The entropy source owing to the flux of heat from the sea surface may be written
where the integral is over the surface area of the control volume,
from the inner radius 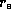 to the outer radius
to the outer radius 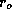 ,
, 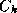 is the surface
exchange coefficient for enthalpy,
is the surface
exchange coefficient for enthalpy, 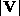 is the mean wind speed at the
standard reference altitude of 10 meters above the surface,
is the mean wind speed at the
standard reference altitude of 10 meters above the surface, 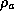 is the air
density at the reference altitude, and
is the air
density at the reference altitude, and  is the specific enthalpy of
moist air, defined
is the specific enthalpy of
moist air, defined
In (28), 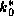 refers to the enthalpy of air saturated at sea
surface temperature and pressure, while
refers to the enthalpy of air saturated at sea
surface temperature and pressure, while 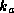 refers to the enthalpy of air at
the reference altitude.
refers to the enthalpy of air at
the reference altitude.
There is also a sink of entropy due to export of heat out of the control volume.
The derivation of this export term is somewhat involved, but here we take a
shortcut by supposing that just inside the outer wall of the control volume,
where air is leaving the control volume, there is an artificial energy sink that
removes the energy that is added in the boundary layer. (A detailed treatment
of the energy cycle which avoids this artifice may be found in Bister and
Emanuel, 1998. [2]) This energy sink occurs in the outflow at a mean
outflow temperature, 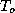 . The heat sink is equivalent to the total
energy sink if we take the outer wall to be far enough from the storm center
that the kinetic energy of the flow there is negligibly small. The entropy sink
owing to this heat sink is then just equal to the heat sink divided by the
outflow temperature:
. The heat sink is equivalent to the total
energy sink if we take the outer wall to be far enough from the storm center
that the kinetic energy of the flow there is negligibly small. The entropy sink
owing to this heat sink is then just equal to the heat sink divided by the
outflow temperature:
The main irreversible entropy source in the control volume is assumed to arise
from dissipation of the kinetic energy of the wind, and this is assumed to occur
mostly in the boundary layer, at a temperature of 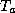 . We neglect other
entropy sources, such as those associated with the evaporation of falling rain
into subsaturated air and dissipation of kinetic energy in the ocean.) The
irreversible entropy source owing to wind dissipation in the boundary layer,
integrated over the control volume, is
. We neglect other
entropy sources, such as those associated with the evaporation of falling rain
into subsaturated air and dissipation of kinetic energy in the ocean.) The
irreversible entropy source owing to wind dissipation in the boundary layer,
integrated over the control volume, is
where 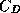 is the surface drag coefficient. Since the entropy,
is the surface drag coefficient. Since the entropy,  is a state
variable, its tendency must vanish in a steady state system, implying that the
sum of (28), (30) and (31) must vanish. We also
suppose that the integrands of all three equations are dominated by their
contribution from near the radius of maximum wind speeds, where both the fluxes
and the dissipation rate are near their maximum values. Assuming that the sum
of the integrands of (28), (30) and (31) vanish at
the radius of maximum winds gives an expression for the maximum wind speed in
the storm:
is a state
variable, its tendency must vanish in a steady state system, implying that the
sum of (28), (30) and (31) must vanish. We also
suppose that the integrands of all three equations are dominated by their
contribution from near the radius of maximum wind speeds, where both the fluxes
and the dissipation rate are near their maximum values. Assuming that the sum
of the integrands of (28), (30) and (31) vanish at
the radius of maximum winds gives an expression for the maximum wind speed in
the storm:
where the notation 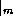 denotes evaluation at the radius of maximum winds.
Although many approximations seem to be involved in the derivation of
(32), the same relation can be derived exactly from consideration of
the dynamics and thermodynamics of tropical cyclones (Bister and Emanuel, 1998
[2]).
denotes evaluation at the radius of maximum winds.
Although many approximations seem to be involved in the derivation of
(32), the same relation can be derived exactly from consideration of
the dynamics and thermodynamics of tropical cyclones (Bister and Emanuel, 1998
[2]).
Several aspects of tropical cyclone energetics are immediately apparent from
(32). First, the maximum specific kinetic energy of the winds is
directly proportional to the thermodynamic disequilibrium between the ocean and
the overlying atmosphere, as expressed by the enthalpy difference
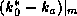 . As we saw in lecture 2, this difference arises from the
greenhouse effect and is also inversely proportional to the mean wind speed in
the tropical lower atmosphere. Second, the enthalpy difference is multiplied by
a thermodynamic efficiency,
. As we saw in lecture 2, this difference arises from the
greenhouse effect and is also inversely proportional to the mean wind speed in
the tropical lower atmosphere. Second, the enthalpy difference is multiplied by
a thermodynamic efficiency, 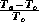 . This is greater than the
classical Carnot efficiency, which is
. This is greater than the
classical Carnot efficiency, which is 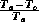 , because in the case
of a tropical cyclone, some of the work produced by the cycle is actually
recycled into the heat engine, whereas in the Carnot cycle, the work is assumed
to be done on an external system. The recycling is possible because dissipation
of kinetic energy occurs at the high temperature reservoir, so that heat of
dissipation is put back into the system. Finally, the maximum wind speed is
proportional to the ratio of the exchange coefficients of enthalpy and
momentum and does not otherwise depend on their actual values.
, because in the case
of a tropical cyclone, some of the work produced by the cycle is actually
recycled into the heat engine, whereas in the Carnot cycle, the work is assumed
to be done on an external system. The recycling is possible because dissipation
of kinetic energy occurs at the high temperature reservoir, so that heat of
dissipation is put back into the system. Finally, the maximum wind speed is
proportional to the ratio of the exchange coefficients of enthalpy and
momentum and does not otherwise depend on their actual values.
Can one actually use (32) to estimate the maximum wind speeds in a
tropical cyclone, given information about the environment in which it exists?
To do so, we need know values of the various parameters that appear in
(32). First, we observe that 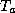 is usually close to the sea
surface temperature, though evaporation of sea spray and adiabatic cooling as
air flows toward lower pressure can cause the air temperature to be a few
degrees K less than that of the ocean. If we attempt to use (32) to
estimate an upper bound on tropical cyclone intensity, than it is
appropriate to assume that
is usually close to the sea
surface temperature, though evaporation of sea spray and adiabatic cooling as
air flows toward lower pressure can cause the air temperature to be a few
degrees K less than that of the ocean. If we attempt to use (32) to
estimate an upper bound on tropical cyclone intensity, than it is
appropriate to assume that 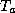 is no greater than the sea surface temperature.
As we shall see in Lecture 5, the sea surface temperature is itself affected by
the passage of tropical cyclones, cooling by as much as 5 K. Again, an upper
bound on tropical cyclone intensity can be estimated by assuming fixed sea
surface temperature.
is no greater than the sea surface temperature.
As we shall see in Lecture 5, the sea surface temperature is itself affected by
the passage of tropical cyclones, cooling by as much as 5 K. Again, an upper
bound on tropical cyclone intensity can be estimated by assuming fixed sea
surface temperature.
Estimating the outflow temperature, 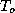 , is straightforward if we know the
vertical temperature structure of the environment of the tropical cyclone.
Tropical cyclones are subcritical vortices, in the sense that the
important atmospheric signal propagators, which are inertia-gravity waves, can
propagate in against the outflow to influence the structure of the core of the
storm. (Some tornadoes, on the other hand, are supercritical vortices in this
sense, so that internal shocks can occur.) The subcriticality of tropical
cyclones means that the isentropic surfaces rising in the core of the storm must
blend in smoothly with the unperturbed environment of the storms. This means,
simply stated, that the air will rise to that altitude at which its temperature
is equal to that of the unperturbed environment. Thus, if we know the entropy
of the air rising in the core of the storm and we know the entropy profile of
the environment, we can estimate the outflow temperature. If the air rises into
the lower stratosphere, then it is particularly straightforward to estimate the
outflow temperature, because the lower stratosphere is practically isothermal.
(In the simple model we will use in lab, the outflow temperature is a specified
constant.)
, is straightforward if we know the
vertical temperature structure of the environment of the tropical cyclone.
Tropical cyclones are subcritical vortices, in the sense that the
important atmospheric signal propagators, which are inertia-gravity waves, can
propagate in against the outflow to influence the structure of the core of the
storm. (Some tornadoes, on the other hand, are supercritical vortices in this
sense, so that internal shocks can occur.) The subcriticality of tropical
cyclones means that the isentropic surfaces rising in the core of the storm must
blend in smoothly with the unperturbed environment of the storms. This means,
simply stated, that the air will rise to that altitude at which its temperature
is equal to that of the unperturbed environment. Thus, if we know the entropy
of the air rising in the core of the storm and we know the entropy profile of
the environment, we can estimate the outflow temperature. If the air rises into
the lower stratosphere, then it is particularly straightforward to estimate the
outflow temperature, because the lower stratosphere is practically isothermal.
(In the simple model we will use in lab, the outflow temperature is a specified
constant.)
Unfortunately, we know almost nothing about the values of 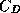 and
and 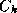 in the
regions of very strong winds. It is difficult to infer these quantities from
direct measurements, and so far we have no reliable estimates at wind speeds
greater than about
in the
regions of very strong winds. It is difficult to infer these quantities from
direct measurements, and so far we have no reliable estimates at wind speeds
greater than about 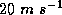 . We do know from photographs of the sea
surface that it becomes extremely complex at higher winds speeds. At winds
speeds greater than about
. We do know from photographs of the sea
surface that it becomes extremely complex at higher winds speeds. At winds
speeds greater than about 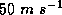 , the sea surface becomes completely
white because of the abundance of foam and spray. At higher wind speeds, the
surface is replaced by an emulsion through which there is a gradual transition
from continuous liquid water, to bubble-filled water, to spray-filled air to
continuous air. We have no good theory for enthalpy or momentum transfer in
these conditions. This is one of the great outstanding impediments to
understanding and predicting tropical cyclone behavior. For lack of better
knowledge, we shall assume that the transfer coefficients are equal at high wind
speed.
, the sea surface becomes completely
white because of the abundance of foam and spray. At higher wind speeds, the
surface is replaced by an emulsion through which there is a gradual transition
from continuous liquid water, to bubble-filled water, to spray-filled air to
continuous air. We have no good theory for enthalpy or momentum transfer in
these conditions. This is one of the great outstanding impediments to
understanding and predicting tropical cyclone behavior. For lack of better
knowledge, we shall assume that the transfer coefficients are equal at high wind
speed.
Finally, to estimate 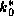 and
and 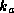 , we need to estimate the surface pressure
and the humidity at the radius of maximum winds. To see this, we first use the
definition of specific enthalpy, (29), to write
, we need to estimate the surface pressure
and the humidity at the radius of maximum winds. To see this, we first use the
definition of specific enthalpy, (29), to write
where we have assumed that the air temperature is equal to the sea
surface temperature, and 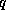 is the specific humidity, which is the mass
of water vapor per unit mass of air. Using the ideal gas law, we can write
is the specific humidity, which is the mass
of water vapor per unit mass of air. Using the ideal gas law, we can write
where 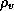 is the water vapor density,
is the water vapor density, 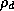 is the density of dry air,
is the density of dry air,
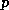 is the total air pressure,
is the total air pressure,  is the partial pressure of water vapor (also
called, simply, the vapor pressure, and
is the partial pressure of water vapor (also
called, simply, the vapor pressure, and  is the ratio of the
molecular weight of water to that of dry air. (This has the value of 0.622 for
atmospheric composition.) Since, in the atmosphere,
is the ratio of the
molecular weight of water to that of dry air. (This has the value of 0.622 for
atmospheric composition.) Since, in the atmosphere, 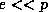 , we can use
(34) to write (33) approximately as
, we can use
(34) to write (33) approximately as
Finally, defining the relative humidity, 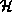 , as
, as 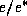 , we may
write (35) as
, we may
write (35) as
Thus (32) becomes
Note that, by the Clausius-Clapeyron equation, 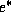 is a function of
temperature alone, so if we know the sea surface temperature, we can calculate
it. We estimate
is a function of
temperature alone, so if we know the sea surface temperature, we can calculate
it. We estimate 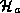 by assuming that it is the same as in the ambient
environment. That is, we assume that the relative humidity is constant in the
inflow, up to the outer edge of the eyewall. Still, we need to know the air
pressure,
by assuming that it is the same as in the ambient
environment. That is, we assume that the relative humidity is constant in the
inflow, up to the outer edge of the eyewall. Still, we need to know the air
pressure, 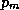 , at the radius of maximum winds, if we want to estimate the
maximum wind speed. On the other hand, the principal reason for wanting to know
the wind speed is because of the force that the wind exerts on objects. The
force per unit area,
, at the radius of maximum winds, if we want to estimate the
maximum wind speed. On the other hand, the principal reason for wanting to know
the wind speed is because of the force that the wind exerts on objects. The
force per unit area, 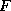 , that wind exerts on an object is proportional to
, that wind exerts on an object is proportional to 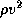 , where
, where 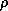 is the air density. Using the ideal gas law and (37),
is the air density. Using the ideal gas law and (37),
where 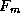 is the force per unit area exerted by the wind where its
value is a maximum. (The actual force per unit area includes a dimensionless
constant that depends on the aerodynamic shape of the object.) From (38)
we see that we now have a closed expression for the force of the wind. From
this we can define a ``dynamical wind" speed that is the wind speed which, at a
given reference air pressure, exerts the same force as the observed wind at the
observed pressure:
is the force per unit area exerted by the wind where its
value is a maximum. (The actual force per unit area includes a dimensionless
constant that depends on the aerodynamic shape of the object.) From (38)
we see that we now have a closed expression for the force of the wind. From
this we can define a ``dynamical wind" speed that is the wind speed which, at a
given reference air pressure, exerts the same force as the observed wind at the
observed pressure:
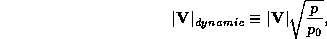
where 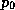 is the reference pressure. Using this in (37) gives
an expression for the dynamical wind speed:
is the reference pressure. Using this in (37) gives
an expression for the dynamical wind speed:
This is a useful expression because it allows us to calculate a wind speed that is representative of the wind force we would experience at a standard reference pressure. Nevertheless, there are other reasons why we might want to know the actual wind speed, and also the pressure, particularly because pressure is often easier to measure than wind. We shall pursue this goal in the next lecture.