Lecture 5: Physics of Mature Tropical Cyclones, II



Next: Lecture 6: Tropical
Up: Tropical Cyclones
Previous: Lecture 4: Physics
In the last lecture, we derived an expression, (37), for the maximum wind
speed in mature tropical cyclones, which depends, among other things, on the
surface pressure, 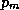 , at the radius of maximum winds. To obtain the wind
speed and pressure separately, we need another relationship between wind and
pressure to complement (37). Here, we need to make a more detailed
analysis of the dynamics of tropical cyclones. We begin with the assumption,
well verified by observations, that the basic wind and pressure fields in
tropical cyclones are in a state of hydrostatic and gradient wind balance, as
expressed by (1) and (2). Cross-differentiating to eliminate
, at the radius of maximum winds. To obtain the wind
speed and pressure separately, we need another relationship between wind and
pressure to complement (37). Here, we need to make a more detailed
analysis of the dynamics of tropical cyclones. We begin with the assumption,
well verified by observations, that the basic wind and pressure fields in
tropical cyclones are in a state of hydrostatic and gradient wind balance, as
expressed by (1) and (2). Cross-differentiating to eliminate
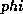 gives
gives
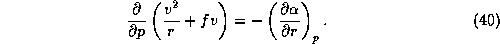
We next use Maxwell's relation, (19), to express the specific volume,
 , in terms of entropy,
, in terms of entropy,  , in (40):
, in (40):
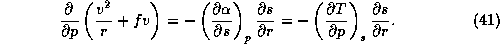
Now we have expressed the right-hand side of the thermal wind equation in terms
of the conserved variable  . We can also express the left-hand side of
(41) in terms of another conserved variable: the angular momentum per
unit mass,
. We can also express the left-hand side of
(41) in terms of another conserved variable: the angular momentum per
unit mass, 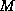 :
:
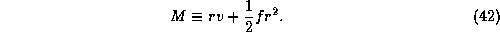
It is easy to show that 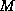 is conserved for axisymmetric displacements in the
absence of friction. If we replace
is conserved for axisymmetric displacements in the
absence of friction. If we replace  by
by 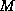 in (41) we get
in (41) we get
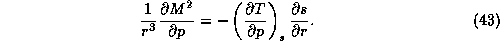
We next assume that surfaces of constant  and of constant
and of constant 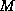 are congruent.
In the eyewall, this will be so because both
are congruent.
In the eyewall, this will be so because both  and
and 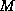 are conserved following
the upflowing air. Elsewhere, it turns out that the congruency of the two
surfaces constitutes a generalized condition for neutral stability with respect
to convection in the presence of centrifugal as well as gravitational forces.
This critical condition appears to be well satisfied in ``full physics"
numerical simulations of tropical cyclones (Rotunno and Emanuel, 1987)
[8]. This condition allows us to write (43) as
are conserved following
the upflowing air. Elsewhere, it turns out that the congruency of the two
surfaces constitutes a generalized condition for neutral stability with respect
to convection in the presence of centrifugal as well as gravitational forces.
This critical condition appears to be well satisfied in ``full physics"
numerical simulations of tropical cyclones (Rotunno and Emanuel, 1987)
[8]. This condition allows us to write (43) as
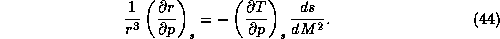
This may be regarded as an equation for the slope of  and
and 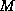 surfaces.
Since the
surfaces.
Since the  and
and 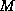 surfaces are congruent, the two quantities are just
functions of one another. Thus we may integrate (44) up along
surfaces are congruent, the two quantities are just
functions of one another. Thus we may integrate (44) up along  surfaces, from their base in the boundary layer to the point at which they
intersect the tropopause, to get
surfaces, from their base in the boundary layer to the point at which they
intersect the tropopause, to get
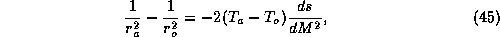
where 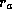 and
and 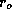 are the radii of particular
are the radii of particular  or
or 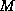 surfaces
where they intersect, respectively, the surface and the tropopause. In a
well-developed tropical cyclone, these surfaces flare out to very large radii at
the tropopause, so we can neglect the second term on the right of (45) in
comparison to the first term. Thus, in the boundary layer, we may write
(45) as
surfaces
where they intersect, respectively, the surface and the tropopause. In a
well-developed tropical cyclone, these surfaces flare out to very large radii at
the tropopause, so we can neglect the second term on the right of (45) in
comparison to the first term. Thus, in the boundary layer, we may write
(45) as
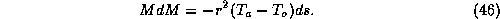
We cannot quite integrate (46) because of the 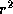 term in it. But it
turns out that we can express (46) in terms of perfect differentials of
some other quantities. First, we substitute (42) for
term in it. But it
turns out that we can express (46) in terms of perfect differentials of
some other quantities. First, we substitute (42) for 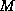 in (46):
in (46):
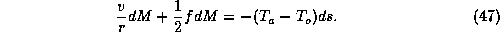
Now we again substitute (42) for 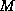 in the first term in (47) and
also make use of (2) expressing gradient wind balance, to get
in the first term in (47) and
also make use of (2) expressing gradient wind balance, to get
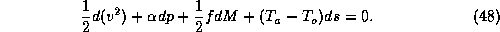
Finally, we make use of the ideal gas law, (3), for  and once again
assume the constancy of both
and once again
assume the constancy of both 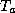 and
and 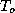 to get
to get
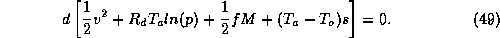
This is the sought-for second relationship between pressure, velocity and
specific humidity. Integrating it from the environment of the storm inward to
the radius of maximum winds, and using (9) to express the entropy,  in
terms of other variables gives
in
terms of other variables gives
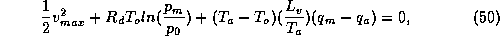
where 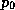 is the ambient surface pressure,
is the ambient surface pressure, 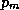 and
and 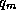 are the
surface pressure and specific humidity at the radius of maximum winds, and
are the
surface pressure and specific humidity at the radius of maximum winds, and 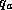 is the ambient boundary layer specific humidity. In writing (50) we have
neglected the Coriolis term, which is small unless the storm extends to very
large radii, and another small term proportional to
is the ambient boundary layer specific humidity. In writing (50) we have
neglected the Coriolis term, which is small unless the storm extends to very
large radii, and another small term proportional to 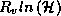 . Now remember that we have assumed that the relative humidity
is constant between the environment and the radius of maximum winds. Using this
together with (34), under the approximation that
. Now remember that we have assumed that the relative humidity
is constant between the environment and the radius of maximum winds. Using this
together with (34), under the approximation that 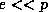 , gives
, gives
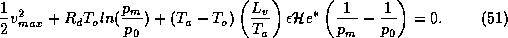
Given the quantities 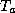 ,
, 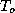 ,
, 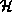 and
and 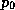 , (51) and (37)
can be solved for both
, (51) and (37)
can be solved for both 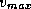 and
and 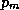 . Eliminating
. Eliminating 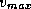 between the
two yields a transcendental equation:
between the
two yields a transcendental equation:
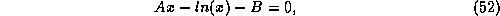
where 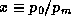 and
and
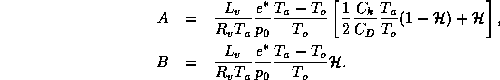
By plotting the two curves 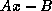 and
and 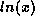 , it is easy to see that (52)
has two solutions, one solution, or no solutions, depending on the values of
, it is easy to see that (52)
has two solutions, one solution, or no solutions, depending on the values of 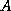 and
and 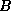 . Once (52) is solved, the result can be substituted into (37)
to find the maximum wind speed.
. Once (52) is solved, the result can be substituted into (37)
to find the maximum wind speed.
Before showing solutions of (52), there is one other quantity that is
useful to derive, because it has become routine to measure it from
reconnaissance aircraft: the central pressure. (Recall that the solution of
(52) is for the surface pressure at the radius of maximum winds.) To
explore the pressure distribution inside the radius of maximum winds, it would
be necessary to discuss the fascinating dynamics of the eye, which we deem
beyond the scope of this short course. Instead, we take a short cut by noting
that, in most cases, the observed wind distribution inside the radius of maximum
winds is not far from that of solid body rotation, in which the azimuthal wind
speed increases linearly with radius. If we assume that this is so, we can
simply integrate the gradient wind balance relation, (2), inward from the
radius of maximum winds to the storm center. In doing so, we neglect the
Coriolis term in (2), which is small compared to the centrifugal term in the
eye. Thus we have
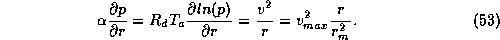
Integrating this inward from 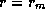 to
to 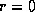 gives
gives
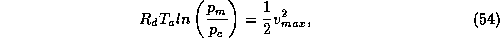
where 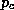 is the central pressure. Note that (54) is
independent of the radius of maximum winds. Given the solution for
is the central pressure. Note that (54) is
independent of the radius of maximum winds. Given the solution for 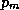 , and
assuming that
, and
assuming that 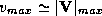 , (54) can be solved for
, (54) can be solved for
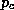 . Thus equations (37), (52) and (54) can be solved for the
pressure at the radius of maximum winds, the maximum winds speed, and the
central pressure. We note in passing that, once this is done, we can integrate
(49) coupled with (2) to find the boundary layer pressure and wind
outside the radius of maximum winds, while the assumption of solid body rotation
and (53) gives the pressure and wind inside the radius of maximum winds.
Then given these, (44) can be integrated upward along angular momentum
surfaces to give the wind and entropy distributions between the boundary layer
and the top of the storm. This was done by Emanuel (1986) [3].
. Thus equations (37), (52) and (54) can be solved for the
pressure at the radius of maximum winds, the maximum winds speed, and the
central pressure. We note in passing that, once this is done, we can integrate
(49) coupled with (2) to find the boundary layer pressure and wind
outside the radius of maximum winds, while the assumption of solid body rotation
and (53) gives the pressure and wind inside the radius of maximum winds.
Then given these, (44) can be integrated upward along angular momentum
surfaces to give the wind and entropy distributions between the boundary layer
and the top of the storm. This was done by Emanuel (1986) [3].
As mentioned before, (52) has no solutions, one solution or two solutions,
depending on the values of 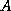 abd
abd 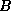 . Also, because of the way it has been
defined,
. Also, because of the way it has been
defined,  is greater than or equal to 1. It is possible to show that, when
two solutions exist, the smaller of the two is the only stable, physically
realizable solution. We present solutions to this set of equations, showing the
smaller root where it exists, in Figure 5.1 and Figure 5.2. The maximum wind
speed and central surface pressure are shown as functions of
is greater than or equal to 1. It is possible to show that, when
two solutions exist, the smaller of the two is the only stable, physically
realizable solution. We present solutions to this set of equations, showing the
smaller root where it exists, in Figure 5.1 and Figure 5.2. The maximum wind
speed and central surface pressure are shown as functions of 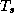 and
and 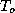 for
given values of
for
given values of 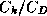 and
and 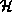 . (The air temperature,
. (The air temperature, 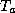 , has been
assumed to equal the sea surface temperature,
, has been
assumed to equal the sea surface temperature, 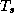 .) Note that the maximum
intensity of the storm increases with the sea surface temperature and decreases
with the outflow temperature. In tropical cyclones, typical values of
.) Note that the maximum
intensity of the storm increases with the sea surface temperature and decreases
with the outflow temperature. In tropical cyclones, typical values of 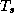 and
and
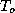 are, respectively, around 300 K and 200 K (27 C and -73 C). Also note the
existence of a ``hypercane" regime in which there are no solutions to (52).
In this regime, the energy cycle of the tropical cyclone is unstable. As the
intensity of the storm increases, the surface pressure falls, and this increases
the saturation enthalpy and entropy of the sea surface, which depends on
pressure. This creates the potential for greater heat input into the system.
In the normal tropical cyclone regime, this positive feedback is countered by
the negative feedback owing to dissipation, which increases as the cube of the
surface wind speed. But in the hypercane regime, the positive feedback is
overwhelming, and the system runs away. Emanuel et al. (1995) [5]
postulated that hypercanes might form where bolide impacts with ocean or large
undersea volcanic eruptions locally heat sea water to values that are
supercritical for hypercanes, and used a ``full-physics" numerical model to
simulate hypercanes. One property of such storms is that they penetrate well up
into the stratosphere, where they can deposit large quantities of water. (The
stratosphere is normally very dry.) Chemical reactions would then rapidly
destroy the ozone layer. We postulated that this might serve as a link between
past massive bolide impacts and mass species extinctions, such as occurred at
the end of the Cretaceous. Hypercanes also produce supersonic wind speeds,
violating some routine assumptions that were made in the numerical model, so
more comprehensive simulations ought to be made using a code capable of
simulating supersonic flows.
are, respectively, around 300 K and 200 K (27 C and -73 C). Also note the
existence of a ``hypercane" regime in which there are no solutions to (52).
In this regime, the energy cycle of the tropical cyclone is unstable. As the
intensity of the storm increases, the surface pressure falls, and this increases
the saturation enthalpy and entropy of the sea surface, which depends on
pressure. This creates the potential for greater heat input into the system.
In the normal tropical cyclone regime, this positive feedback is countered by
the negative feedback owing to dissipation, which increases as the cube of the
surface wind speed. But in the hypercane regime, the positive feedback is
overwhelming, and the system runs away. Emanuel et al. (1995) [5]
postulated that hypercanes might form where bolide impacts with ocean or large
undersea volcanic eruptions locally heat sea water to values that are
supercritical for hypercanes, and used a ``full-physics" numerical model to
simulate hypercanes. One property of such storms is that they penetrate well up
into the stratosphere, where they can deposit large quantities of water. (The
stratosphere is normally very dry.) Chemical reactions would then rapidly
destroy the ozone layer. We postulated that this might serve as a link between
past massive bolide impacts and mass species extinctions, such as occurred at
the end of the Cretaceous. Hypercanes also produce supersonic wind speeds,
violating some routine assumptions that were made in the numerical model, so
more comprehensive simulations ought to be made using a code capable of
simulating supersonic flows.
Routine atmospheric data together with sea surface temperature records can be
used to calculate the maximum wind speeds and minimum central pressures possible
in tropical cyclones in the present climate. Now go to the potential intensity
climatology site and look at the various distributions. It is helpful to bear
in mind that the minimum central pressure ever measured in a northwest Pacific
typhoon was 870 mb, while the lowest pressure in the North Atlantic was 888 mb.
Today's potential intensity calculations are shown at this website. Here the
atmospheric temperature profiles are updated daily while the ocean temperatures
are updated weekly.
How do the intensities of actual tropical cyclones compare with potential
intensities? There are reliable records of tropical cyclones in the North
Atlantic going back to about 1958, when reconnaissance aircraft first began to
directly measure wind speeds. In the western North Pacific, there was routine
aircraft reconnaissance from the 1960's through 1987. tropical cyclone
positions and maximum wind speeds are recorded every 6 hours. We can estimate
the potential maximum wind speed from its monthly mean value, which was
calculated using about 20 years of atmospheric and sea surface temperature data.
We take each 6 hours intensity report and divide it by the climatological
potential intensity for that position and that month to create a normalized
intensity,  . We then create a cumulative distribution function, or CDF, by
summing the total number of observations of normalized intensity exceeding
. We then create a cumulative distribution function, or CDF, by
summing the total number of observations of normalized intensity exceeding  for each value of
for each value of  . We do this only for those storms for which the
potential maximum wind speed exceeds
. We do this only for those storms for which the
potential maximum wind speed exceeds 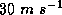 to avoid counting those
storms that have moved over land or cold water and are in the process of rapid
decay. The results are shown for the North Atlantic and western North Pacific
in Figure 5.3 and Figure 5.4, respectively. Also shown is a curve that seems to
fit both data sets quite well; it has the functional form
to avoid counting those
storms that have moved over land or cold water and are in the process of rapid
decay. The results are shown for the North Atlantic and western North Pacific
in Figure 5.3 and Figure 5.4, respectively. Also shown is a curve that seems to
fit both data sets quite well; it has the functional form
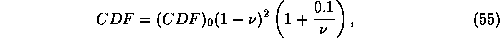
where 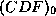 is a constant that is related to the total frequency
of events of all normalized intensities.
is a constant that is related to the total frequency
of events of all normalized intensities.
We have essentially no understanding of why the data fit a curve like that given
by (55). Note that no storms have intensities that exceed the potential
intensity by any significant amount, but the vast majority of storms fall well
short of their potential. Some of this is owing to the fact that some of the
storms in the record are in the process of intensifying, but even if we confine
the data to storms in nearly steady states, a curve not much different from
(55) results. On the other hand, virtually all numerical simulations of
tropical cyclones using axisymmetric models manage to spin up storms right to
their potential intensity. Why are storms in nature less intense than the model
storms? This is a point we shall return to in a future lecture.



Next: Lecture 6: Tropical
Up: Tropical Cyclones
Previous: Lecture 4: Physics
Kerry Emanuel
Mon Apr 13 10:50:48 EDT 1998
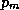 , at the radius of maximum winds. To obtain the wind
speed and pressure separately, we need another relationship between wind and
pressure to complement (37). Here, we need to make a more detailed
analysis of the dynamics of tropical cyclones. We begin with the assumption,
well verified by observations, that the basic wind and pressure fields in
tropical cyclones are in a state of hydrostatic and gradient wind balance, as
expressed by (1) and (2). Cross-differentiating to eliminate
, at the radius of maximum winds. To obtain the wind
speed and pressure separately, we need another relationship between wind and
pressure to complement (37). Here, we need to make a more detailed
analysis of the dynamics of tropical cyclones. We begin with the assumption,
well verified by observations, that the basic wind and pressure fields in
tropical cyclones are in a state of hydrostatic and gradient wind balance, as
expressed by (1) and (2). Cross-differentiating to eliminate
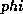 gives
gives
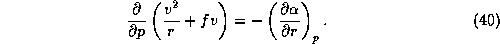
 , in terms of entropy,
, in terms of entropy,  , in (
, in (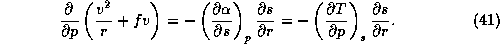
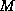 :
:
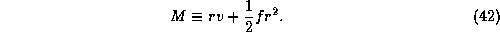
 by
by 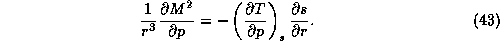
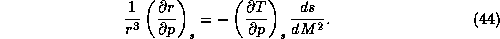
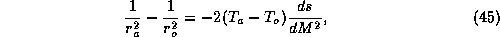
 and
and 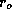 are the radii of particular
are the radii of particular 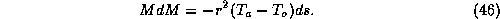
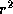 term in it. But it
turns out that we can express (
term in it. But it
turns out that we can express (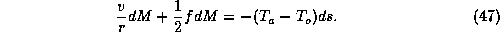
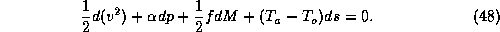
 and once again
assume the constancy of both
and once again
assume the constancy of both  and
and  to get
to get
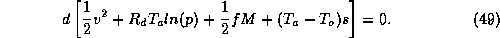
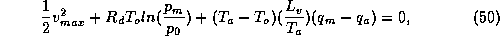
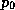 is the ambient surface pressure,
is the ambient surface pressure, 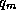 are the
surface pressure and specific humidity at the radius of maximum winds, and
are the
surface pressure and specific humidity at the radius of maximum winds, and 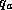 is the ambient boundary layer specific humidity. In writing (
is the ambient boundary layer specific humidity. In writing (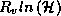 . Now remember that we have assumed that the relative humidity
is constant between the environment and the radius of maximum winds. Using this
together with (
. Now remember that we have assumed that the relative humidity
is constant between the environment and the radius of maximum winds. Using this
together with (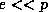 , gives
, gives
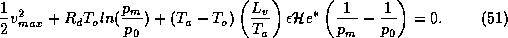
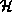 and
and 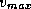 and
and 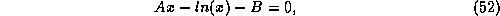
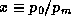 and
and
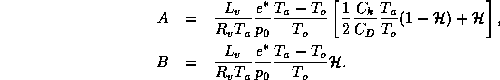
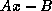 and
and 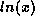 , it is easy to see that (
, it is easy to see that (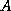 and
and 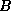 . Once (
. Once (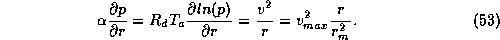
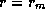 to
to 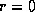 gives
gives
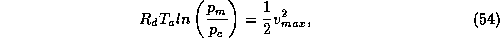
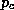 is the central pressure. Note that (
is the central pressure. Note that (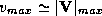 , (
, ( is greater than or equal to 1. It is possible to show that, when
two solutions exist, the smaller of the two is the only stable, physically
realizable solution. We present solutions to this set of equations, showing the
smaller root where it exists, in
is greater than or equal to 1. It is possible to show that, when
two solutions exist, the smaller of the two is the only stable, physically
realizable solution. We present solutions to this set of equations, showing the
smaller root where it exists, in 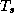 and
and 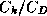 and
and  . We then create a cumulative distribution function, or CDF, by
summing the total number of observations of normalized intensity exceeding
. We then create a cumulative distribution function, or CDF, by
summing the total number of observations of normalized intensity exceeding 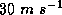 to avoid counting those
storms that have moved over land or cold water and are in the process of rapid
decay. The results are shown for the North Atlantic and western North Pacific
in
to avoid counting those
storms that have moved over land or cold water and are in the process of rapid
decay. The results are shown for the North Atlantic and western North Pacific
in 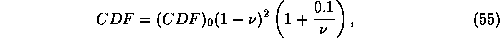
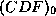 is a constant that is related to the total frequency
of events of all normalized intensities.
is a constant that is related to the total frequency
of events of all normalized intensities.