Interlude: A simple tropical cyclone model



Next: Field experiment
Up: Lecture 6: Tropical
Previous: Lecture 6: Tropical
Here is a brief description of the model we will be using in lab. A complete
description of the construction of the model may be found at this
site. The published version is Emanuel (1995). [4]
The model is predicated on the approximations that the tropical cyclone vortex
is nearly in hydrostatic and gradient wind balance, as expressed by (1) and
(2), and that above the boundary layer, surfaces of constant saturation
entropy, 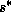 , and angular momentum,
, and angular momentum, 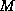 , are congruent, so that (45)
applies everywhere. This is equivalent to assuming that slantwise moist
convection keeps the atmosphere nearly neutral to such convection. In fact, we
take advantage of symmetry and conservation of angular momentum by phrasing the
model not in physical coordinates, but in a new coordinate system whose radial
coordinate is proportional to angular momentum. Specifically, we define the
potential radius,
, are congruent, so that (45)
applies everywhere. This is equivalent to assuming that slantwise moist
convection keeps the atmosphere nearly neutral to such convection. In fact, we
take advantage of symmetry and conservation of angular momentum by phrasing the
model not in physical coordinates, but in a new coordinate system whose radial
coordinate is proportional to angular momentum. Specifically, we define the
potential radius, 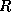 , such that
, such that
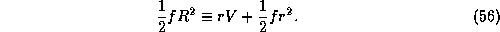
There are several powerful advantages of using this conserved variable as a
model coordinate. First, above the boundary layer (in which friction with the
surface causes flow across angular momentum surfaces), angular momentum surfaces
move with the flow, so that there is no advection in angular momentum
coordinates. The nonlinear advection terms are usually the most problematic to
deal with in fluid systems. Second, in a fully developed cyclone, there is a
large gradient of angular momentum in the eyewall, so one gets very high radial
resolution there by using angular momentum coordinates. Finally, as mentioned
previously, convection acts to keep 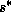 constant along angular momentum
surfaces, which means in the vertical within an angular momentum coordinate
system.
constant along angular momentum
surfaces, which means in the vertical within an angular momentum coordinate
system.
In angular momentum coordinates, the physical radius ,  , of angular momentum
surfaces at each model level becomes a dependent variable. If we know
, of angular momentum
surfaces at each model level becomes a dependent variable. If we know  along
each
along
each 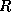 surface, then we can easily invert (56) to get the swirling flow
component,
surface, then we can easily invert (56) to get the swirling flow
component, 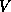 . So we have to come up with a prediction equation for
. So we have to come up with a prediction equation for  . To
do this, we start with (44), which, using
. To
do this, we start with (44), which, using 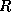 instead of
instead of 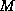 , is
, is
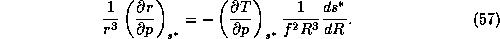
If we now differentiate this in time, holding the other coordinates, pressure
and angular momentum, fixed, we get
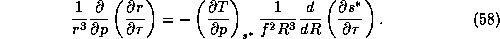
Here, partial differentiation in  is defined to hold
is defined to hold 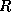 and
and 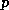 fixed,
and we have ignored the time dependence of
fixed,
and we have ignored the time dependence of 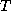 at fixed pressure. The whole
problem reduces to finding the time dependence of
at fixed pressure. The whole
problem reduces to finding the time dependence of 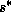 ; given that, (58)
can be integrated upward to find the time-dependence of
; given that, (58)
can be integrated upward to find the time-dependence of  . (A boundary
condition is needed for this upward integration; it is supplied by conservation
of mass. Were it not for friction, the mass inside each
. (A boundary
condition is needed for this upward integration; it is supplied by conservation
of mass. Were it not for friction, the mass inside each 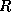 surface would be
conserved and this would be enough to determine the integration constant when
integrating (58) in pressure. Friction does cause mass flow across
surface would be
conserved and this would be enough to determine the integration constant when
integrating (58) in pressure. Friction does cause mass flow across 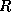 surfaces, however, and this must be accounted for.)
surfaces, however, and this must be accounted for.)
We can see from (58) that the problem of predicting the physical radius of
angular momentum surfaces at each altitude, which is equivalent to predicting
the swirling component of the wind, reduces to the problem of predicting the
saturation moist entropy, 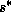 , as a function of time and
, as a function of time and 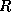 . This is where
convection and thermodynamics enter the problem. There are three main processes
that change
. This is where
convection and thermodynamics enter the problem. There are three main processes
that change 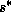 :
:
- Heating by moist convection
- Compressional warming by
large-scale subsidence in unsaturated air
- Radiative cooling
The heating by moist convection is, of course, critical. What is done here is
to assume that everywhere that the actual entropy of the boundary layer, 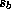 ,
exceeds the saturation entropy
,
exceeds the saturation entropy 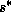 above the boundary layer, convection will
act to reduce their difference. Thus we calculate a convective mass flux along
above the boundary layer, convection will
act to reduce their difference. Thus we calculate a convective mass flux along
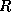 surfaces that is proportional to the difference between
surfaces that is proportional to the difference between 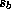 and
and 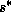 .
This mass flux increases
.
This mass flux increases 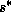 aloft and, because it is associated with
downdrafts, generally reduces
aloft and, because it is associated with
downdrafts, generally reduces 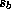 by importing lower values of entropy from
aloft. The stronger the downdrafts relative to the updrafts, the less heating
aloft and the greater the reduction of boundary layer entropy. One of the
most important aspects of representing the cumulus convection is determining the
relative strengths of updrafts and downdrafts. In this case, the relative
strength of the downdrafts is a function of how dry the air is just above the
boundary layer; this in turn can be determined if the actual (as opposed to
saturation) entropy just above the boundary layer is known. To predict the
evolution of the tropical cyclone vortex, it is necessary to predict the entropy
of the lower to middle troposphere. The present model represents this lower
tropospheric entropy as a single layer average. This entropy is affected by
vertical advection and by cumulus convection.
by importing lower values of entropy from
aloft. The stronger the downdrafts relative to the updrafts, the less heating
aloft and the greater the reduction of boundary layer entropy. One of the
most important aspects of representing the cumulus convection is determining the
relative strengths of updrafts and downdrafts. In this case, the relative
strength of the downdrafts is a function of how dry the air is just above the
boundary layer; this in turn can be determined if the actual (as opposed to
saturation) entropy just above the boundary layer is known. To predict the
evolution of the tropical cyclone vortex, it is necessary to predict the entropy
of the lower to middle troposphere. The present model represents this lower
tropospheric entropy as a single layer average. This entropy is affected by
vertical advection and by cumulus convection.
The entropy of the boundary layer is increased by surface fluxes and by
dissipation of kinetic energy owing to friction; it is decreased by radiative
cooling and by the aforementioned import of drier air from above the boundary
layer. Also, friction causes advection of entropy across 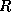 surfaces and this
is accounted for in the model.
surfaces and this
is accounted for in the model.
To predict the compressional heating by large-scale subsidence, we have to
predict the latter. In a balanced model, the vertical motion is actually
implied by the evolution of the balanced motion. To see this in the present
case, we first define a mass streamfunction, 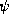 , such that
, such that

and

where  is the radial velocity and
is the radial velocity and  is the ``pressure
velocity", which is just the total time rate of change of pressure following a
sample of air. In
is the ``pressure
velocity", which is just the total time rate of change of pressure following a
sample of air. In 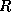 coordinates, it can be shown that
coordinates, it can be shown that
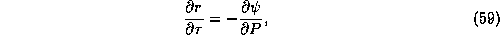
where the upper case 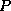 on the right signifies differentiation
holding
on the right signifies differentiation
holding  and
and 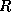 constant. Now if we eliminate
constant. Now if we eliminate  between (57) and
(59), by differentiating the former with respect to
between (57) and
(59), by differentiating the former with respect to  , we get a
differential equation relating
, we get a
differential equation relating 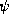 to a function of the time derivative of
to a function of the time derivative of
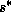 . But, as we just said, the latter will itself be proportional, among
other things, to the rate of compressional warming, which is in turn a function
of
. But, as we just said, the latter will itself be proportional, among
other things, to the rate of compressional warming, which is in turn a function
of 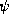 . What we get in the end is an elliptic equation for
. What we get in the end is an elliptic equation for 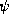 that we
have to solve every time step.
that we
have to solve every time step.
Finally, we have to represent radiative cooling. If there is no radiative
cooling, the model storm eventually chokes on its own heating, since there is
then no way to get rid of it. Here we do exactly the same thing that we
described in the case of the ``full physics" numerical model of Rotunno and
Emanuel (1987) [8]: we relax the given temperature back to the initial
temperature over a fixed time scale, but restrict the maximum rate of cooling.
One last element of the model needs to be mentioned here. There is a tendency
of models phrased in conserved variable coordinates to simulate strong frontogenesis, in which the conserved variable surfaces actually intersect and
then cross each other when back-transformed into physical space. This
represents a real physical process, until the point of frontal collapse when, in
the real world, turbulent diffusion would prevent a total collapse of the front.
The eyewall of a tropical cyclone turns out to be strongly frontogenetic, and to
prevent complete frontal collapse, it is necessary to have some radial
diffusion. We represent radial turbulent fluxes of heat and momentum in this
model in exactly the same way they are represented in the full physics model,
albeit transformed into the new coordinate system.
The structure of the model is shown in Figure 6.3. The vertical discretization
is necessary only to define a boundary layer wherein friction is influential,
and to define the lower tropospheric entropy. It is also used to invert an
elliptic equation for the mass streamfunction. It is not necessary to
discretize the swirling velocity or temperature in the vertical, as the
assumption of slantwise neutrality completely specifies their vertical
structure.
You can now try running this simple model. Ask the instructor or one of the
TA's to show you how to access the model. Or you can download it and run it on
your own machine by clicking here. The
FORTRAN program, which you do not have to change in any way, reads an input file
containing ordinary, ASCII text. This input file controls the model. By
modifying it, you can change the parameters governing the behavior of the
simulated tropical cyclone. Here is what the input file looks like:
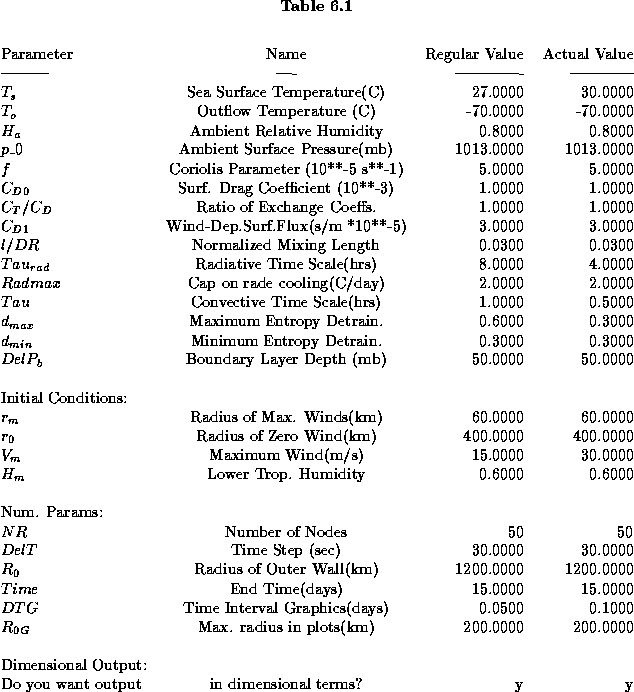
Most of these parameters are self-explanatory or will be covered in lecture.
The third column shows the normal value of the parameter, used in a ``control"
run, while the last column contains the value that is actually used. This last
column is the one you want to change.
While the input file above allows one to specify normal, dimensional
environmental and control parameters, the actual model code is written in
non-dimensional form. It turns out that almost all of the strong dependencies
of the model behavior can be absorbed into a suitable set of nondimensional
parameters. For reference, the way the dependent and independent variables are
normalized is shown in the Table 6.2. The
fundamental parameter is 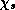 , a measure of the product of the thermodynamic
efficiency of the system and the degree of air-sea thermodynamic disequilibrium.
It has the units of velocity squared, and it turns out that a natural scale for
the maximum swirling velocity is just
, a measure of the product of the thermodynamic
efficiency of the system and the degree of air-sea thermodynamic disequilibrium.
It has the units of velocity squared, and it turns out that a natural scale for
the maximum swirling velocity is just 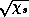 . The radial velocity
scales quite differently, varying as both
. The radial velocity
scales quite differently, varying as both 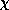 and the drag coefficient with
the surface. It is also inversely proportional to the Coriolis parameter,
and the drag coefficient with
the surface. It is also inversely proportional to the Coriolis parameter, 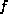 .
The vertical velocity scales as the swirling velocity multiplied by the surface
drag coefficient. There is an outer radial scale that is related to an upper
bound on the geometric size that tropical cyclones can obtain, it is just the
swirling velocity scale divided by the Coriolis parameter. A natural time scale
turns out to be just the radial scale divided by the radial velocity scale.
.
The vertical velocity scales as the swirling velocity multiplied by the surface
drag coefficient. There is an outer radial scale that is related to an upper
bound on the geometric size that tropical cyclones can obtain, it is just the
swirling velocity scale divided by the Coriolis parameter. A natural time scale
turns out to be just the radial scale divided by the radial velocity scale.
The original version of the simple model was written in terms of the
nondimensional variables; the model equations can be viewed at this
site. There is a great advantage in using the nondimensional model,
because many of the sensitivities are absorbed into the nondimensionalization.
For example, it is not necessary to run the nondimensional model more than once
to examine the sensitivity of tropical cyclones to sea surface temperature,
because this sensitivity appears only when one redimensionalizes the output
using Table 6.2. But, to avoid any
confusion, we stick to the dimensional version of the model here.
The evolution of the maximum wind speed in the control run of the model is shown
by the upper solid line in Figure 6.4. The behavior of the model is very
similar to that of the full-physics model, suggesting that we have indeed
captured the essential physics with the simple model. The lowest curve in this
figure shows the evolution of the vortex starting from a much smaller amplitude.
As in the full physics model, the low amplitude vortex decays, showing that this
model is also metastable to tropical cyclones.
It is much easier to do radical surgery on the simple model than on the full
physics model. For example, the critical role of downdrafts in making the model
metastable to tropical cyclones can be tested simply by excising downdrafts from
the model physics. The results of doing this are also shown in Figure 6.4. The
role of downdrafts is paradoxical: they evidently prevent weak disturbances
from amplifying, but they allow strong disturbances to amplify faster than they
would otherwise.
A closer look at how the model is behaving reveals why it does what it does. In
the control experiment, a modest vortex is used to initialize the model. From
the very beginning, surface friction slows down the boundary layer winds. This
reduces the outward acceleration owing to centripetal and Coriolis forces, but
has little direct effect on the radial pressure distribution. Consequently,
gradient balance is destroyed and air accelerates inward until Coriolis
accelerations acting on the radial velocity can balance friction acting on the
swirling velocity component. The inward flowing air must eventually turn upward
so that mass does not accumulate in the boundary layer. This
frictionally-induced upward motion at the top of the boundary layer is called
Ekman pumping.
Ascent of air above the top of the boundary layer would, unimpeded, be
associated with adiabatic cooling. But as soon as the air above the boundary
layer cools, it becomes unstable to convection. So the upward motion leads to
stronger convection. The precipitation generated by the convection causes
downdrafts when it partially evaporates into the subsaturated air of the lower
to middle troposphere, thereby cooling it. These downdrafts import low entropy
air of the lower and middle troposphere into the boundary layer, quenching any
tendency for surface fluxes to increase the entropy there. This is the
quintessential negative feedback mechanism that prevents most arbitrary tropical
disturbances from becoming tropical cyclones.
At the same time that convection is reducing the entropy of the boundary layer,
it is increasing the entropy of the lower and middle troposphere. (Remember
that convection is just a transport mechanism; except for a small contribution
from dissipation of turbulence, clouds just rearrange entropy, they do not
generate it. So if they reduce entropy somewhere, they must increase it
somewhere else to compensate.) If the initial vortex is strong enough, and this
process continues long enough, then eventually, the air in the lower and middle
troposphere becomes so moist that evaporation is reduced and the downdrafts
become weak. What downdrafts still exist are now importing air with only
slightly depressed entropy into the boundary layer. This allows the surface
fluxes to overwhelm the negative effects of downdrafts, so that the boundary
layer entropy begins to increase and the storm intensifies.
This view of the initial vortex evolution is supported by some additional
experiments. By changing the initial entropy deficit of the lower and middle
troposphere, one can examine the sensitivity of the vortex development to the
dryness of that layer, as shown in Figure 6.5. Clearly, the amount of
``gestation" time depends almost linearly on the dryness of the air above the
boundary layer: The drier the air, the longer it takes until ``ignition" of the
heat engine. In another experiment (Figure 6.6), we begin with a state that is
saturated through the whole troposphere out to about 100 km radius. Even a very
weak initial vortex amplifies quite rapidly to hurricane strength.
Given the results of these numerical experiments, we postulate this hypothesis:
A necessary and sufficient condition for the onset of tropical cyclone
intensification is the presence of a mesoscale (order 100 km) region of nearly
saturated air through the lower and middle troposphere. If this turns out to
be true, then we can define genesis as the ignition point at which the
Carnot cycle is turned on, which happens when downdrafts in the core become
sufficiently weak. To test this hypothesis, we conducted a field experiment,
described in the next section.



Next: Field experiment
Up: Lecture 6: Tropical
Previous: Lecture 6: Tropical
Kerry Emanuel
Mon Apr 13 10:50:48 EDT 1998
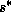 , and angular momentum,
, and angular momentum, 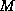 , are congruent, so that (45)
applies everywhere. This is equivalent to assuming that slantwise moist
convection keeps the atmosphere nearly neutral to such convection. In fact, we
take advantage of symmetry and conservation of angular momentum by phrasing the
model not in physical coordinates, but in a new coordinate system whose radial
coordinate is proportional to angular momentum. Specifically, we define the
potential radius,
, are congruent, so that (45)
applies everywhere. This is equivalent to assuming that slantwise moist
convection keeps the atmosphere nearly neutral to such convection. In fact, we
take advantage of symmetry and conservation of angular momentum by phrasing the
model not in physical coordinates, but in a new coordinate system whose radial
coordinate is proportional to angular momentum. Specifically, we define the
potential radius, 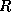 , such that
, such that
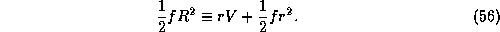
 , of angular momentum
surfaces at each model level becomes a dependent variable. If we know
, of angular momentum
surfaces at each model level becomes a dependent variable. If we know 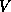 . So we have to come up with a prediction equation for
. So we have to come up with a prediction equation for 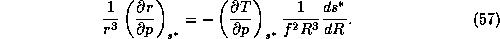
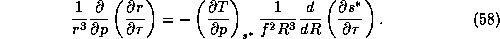
 is defined to hold
is defined to hold 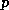 fixed,
and we have ignored the time dependence of
fixed,
and we have ignored the time dependence of 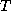 at fixed pressure. The whole
problem reduces to finding the time dependence of
at fixed pressure. The whole
problem reduces to finding the time dependence of 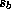 ,
exceeds the saturation entropy
,
exceeds the saturation entropy 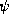 , such that
, such that


 is the radial velocity and
is the radial velocity and  is the ``pressure
velocity", which is just the total time rate of change of pressure following a
sample of air. In
is the ``pressure
velocity", which is just the total time rate of change of pressure following a
sample of air. In 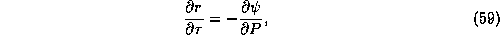
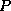 on the right signifies differentiation
holding
on the right signifies differentiation
holding 
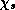 , a measure of the product of the thermodynamic
efficiency of the system and the degree of air-sea thermodynamic disequilibrium.
It has the units of velocity squared, and it turns out that a natural scale for
the maximum swirling velocity is just
, a measure of the product of the thermodynamic
efficiency of the system and the degree of air-sea thermodynamic disequilibrium.
It has the units of velocity squared, and it turns out that a natural scale for
the maximum swirling velocity is just 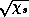 . The radial velocity
scales quite differently, varying as both
. The radial velocity
scales quite differently, varying as both 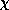 and the drag coefficient with
the surface. It is also inversely proportional to the Coriolis parameter,
and the drag coefficient with
the surface. It is also inversely proportional to the Coriolis parameter, 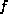 .
The vertical velocity scales as the swirling velocity multiplied by the surface
drag coefficient. There is an outer radial scale that is related to an upper
bound on the geometric size that tropical cyclones can obtain, it is just the
swirling velocity scale divided by the Coriolis parameter. A natural time scale
turns out to be just the radial scale divided by the radial velocity scale.
.
The vertical velocity scales as the swirling velocity multiplied by the surface
drag coefficient. There is an outer radial scale that is related to an upper
bound on the geometric size that tropical cyclones can obtain, it is just the
swirling velocity scale divided by the Coriolis parameter. A natural time scale
turns out to be just the radial scale divided by the radial velocity scale.